湖南省益阳市2022年中考数学试卷

试卷更新日期：2022-08-09 类型：中考真卷

进入出卷网下载

一、单选题

1. 四个实数﹣ $\sqrt{2}$ ， 1，2， $\frac{1}{3}$ 中，比0小的数是（）

A、﹣ $\sqrt{2}$ B、1 C、2 D、 $\frac{1}{3}$

查看试题解析
2. 下列各式中，运算结果等于a²的是（）

A、a³﹣a B、a+a C、a•a D、a⁶÷a³

查看试题解析
3. 若x＝2是下列四个选项中的某个不等式组的一个解，则这个不等式组是（）

A、 ${\begin{array}{l} x < 1 \\ x < - 1 \end{array}$ B、 ${\begin{array}{l} x < 1 \\ x > - 1 \end{array}$ C、 ${\begin{array}{l} x > 1 \\ x < - 1 \end{array}$ D、 ${\begin{array}{l} x > 1 \\ x > - 1 \end{array}$

查看试题解析
4. 若x＝﹣1是方程x²+x+m＝0的一个根，则此方程的另一个根是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
5. 已知一个函数的因变量y与自变量x的几组对应值如表，则这个函数的表达式可以是（）
x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…

A、y＝2x B、y＝x﹣1 C、y＝ $\frac{2}{x}$ D、y＝x²

查看试题解析
6. 在某市组织的物理实验操作考试中，考试所用实验室共有24个测试位，分成6组，同组4个测试位各有一道相同试题，各组的试题不同，分别标记为A，B，C，D，E，F，考生从中随机抽取一道试题，则某个考生抽到试题A的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{24}$

查看试题解析
7. 如图1所示，将长为6的矩形纸片沿虚线折成3个矩形，其中左右两侧矩形的宽相等，若要将其围成如图2所示的三棱柱形物体，则图中a的值可以是（）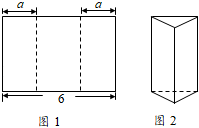

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在▱ABCD中，AB＝8，点E是AB上一点，AE＝3，连接DE，过点C作CF∥DE，交AB的延长线于点F，则BF的长为（）

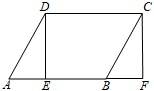A、5 B、4 C、3 D、2

查看试题解析
9. 如图，在△ABC中，BD平分∠ABC，以点A为圆心，以任意长为半径画弧交射线AB，AC于两点，分别以这两点为圆心，以适当的定长为半径画弧，两弧交于点E，作射线AE，交BD于点I，连接CI，以下说法错误的是（）

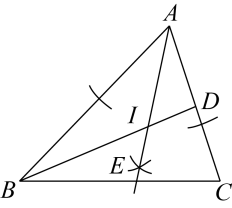A、I到AB，AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A，B，C三点的距离相等

查看试题解析
10. 如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（）

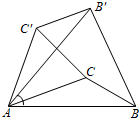A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

11. $\sqrt[3]{- 1}$ 的绝对值是.

查看试题解析
12. 计算： $\frac{2 a}{a - 1}$ ﹣ $\frac{2}{a - 1}$ ＝．

查看试题解析
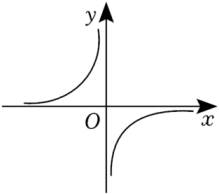
13. 已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m²﹣n²的值是．

查看试题解析
14. 反比例函数y＝ $\frac{k - 2}{x}$ 的图像分布情况如图所示，则k的值可以是（写出一个符合条件的k值即可）．

查看试题解析
15. 如图，PA，PB表示以P为起点的两条公路，其中公路PA的走向是南偏西34 $°$ ，公路PB的走向是南偏东56 $°$ ，则这两条公路的夹角∠APB＝°．

查看试题解析
16. 近年来，洞庭湖区环境保护效果显著，南迁的候鸟种群越来越多．为了解南迁到该区域某湿地的A种候鸟的情况，从中捕捉40只，戴上识别卡并放回；经过一段时间后观察发现，200只A种候鸟中有10只佩有识别卡，由此估计该湿地约有只A种候鸟．

查看试题解析
17. 如图，在Rt△ABC中，∠C＝90°，若sinA＝ $\frac{4}{5}$ ，则cosB＝．

查看试题解析
18. 如图，将边长为3的正方形ABCD沿其对角线AC平移，使A的对应点A′满足AA′＝ $\frac{1}{3}$ AC，则所得正方形与原正方形重叠部分的面积是．

查看试题解析

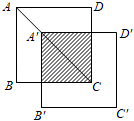
三、解答题

19. 计算：（﹣2022）⁰+6×（﹣ $\frac{1}{2}$ ）+ $\sqrt{8}$ ÷ $\sqrt{2}$ ．

查看试题解析
20. 如图，在Rt△ABC中，∠B＝90°，CD∥AB，DE⊥AC于点E，且CE＝AB．求证：△CED≌△ABC．

查看试题解析
21. 如图，直线y＝ $\frac{1}{2}$ x+1与x轴交于点A，点A关于y轴的对称点为A′，经过点A′和y轴上的点B（0，2）的直线设为y＝kx+b．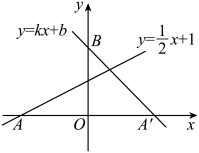

(1)、求点A′的坐标；

(2)、确定直线A′B对应的函数表达式．

查看试题解析
22. 为了加强心理健康教育，某校组织七年级（1）（2）两班学生进行了心理健康常识测试（分数为整数，满分为10分），已知两班学生人数相同，根据测试成绩绘制了如下所示的统计图．

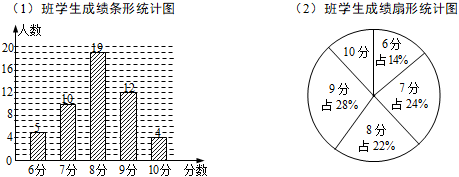(1)、求（2）班学生中测试成绩为10分的人数；

(2)、请确定下表中a，b，c的值（只要求写出求a的计算过程）；
统计量
平均数
众数
中位数
方差
（1）班
8
8
c
1.16
（2）班
a
b
8
1.56

(3)、从上表中选择合适的统计量，说明哪个班的成绩更均匀．

查看试题解析
23. 如图，C是圆O被直径AB分成的半圆上一点，过点C的圆O的切线交AB的延长线于点P，连接CA，CO，CB．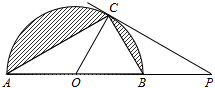

(1)、求证：∠ACO＝∠BCP；

(2)、若∠ABC＝2∠BCP，求∠P的度数；

(3)、在（2）的条件下，若AB＝4，求图中阴影部分的面积（结果保留π和根号）．

查看试题解析
24. 在某市组织的农机推广活动中，甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛．已知乙每小时收割的亩数比甲少40%，两人各收割6亩水稻，乙则比甲多用0.4小时完成任务；甲、乙在收割过程中对应收稻谷有一定的遗落或破损，损失率分别为3%，2%．

(1)、甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻？

(2)、某水稻种植大户有与比赛中规格相同的100亩待收水稻，邀请甲、乙两人操控原收割机一同前去完成收割任务，要求平均损失率不超过2.4%，则最多安排甲收割多少小时？

查看试题解析
25. 如图，在平面直角坐标系xOy中，抛物线E：y＝﹣（x﹣m）²+2m²（m＜0）的顶点P在抛物线F：y＝ax²上，直线x＝t与抛物线E，F分别交于点A，B．

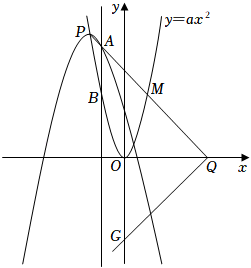(1)、求a的值；

(2)、将A，B的纵坐标分别记为yA，yB，设s＝yA﹣yB，若s的最大值为4，则m的值是多少？

(3)、Q是x轴的正半轴上一点，且PQ的中点M恰好在抛物线F上．试探究：此时无论m为何负值，在y轴的负半轴上是否存在定点G，使∠PQG总为直角？若存在，请求出点G的坐标；若不存在，请说明理由．

查看试题解析
26. 如图，矩形ABCD中，AB＝15，BC＝9，E是CD边上一点（不与点C重合），作AF⊥BE于F，CG⊥BE于G，延长CG至点C′，使C′G＝CG，连接CF，AC′．

(1)、直接写出图中与△AFB相似的一个三角形；

(2)、若四边形AFCC′是平行四边形，求CE的长；

(3)、当CE的长为多少时，以C′，F，B为顶点的三角形是以C′F为腰的等腰三角形？

查看试题解析

统计量	平均数	众数	中位数	方差
（1）班	8	8	c	1.16
（2）班	a	b	8	1.56

x	…	﹣1	0	1	2	…
y	…	﹣2	0	2	4	…