贵州省黔西南州2022年中考数学试卷
试卷更新日期:2022-08-09 类型:中考真卷
一、单选题
-
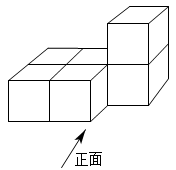
1. 实数的绝对值是( )A、-3 B、±3 C、3 D、2. 如图,是由6个相同的正方体组成的立体图形,它的俯视图是( )
 A、
A、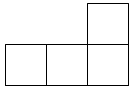 B、
B、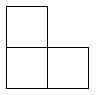 C、
C、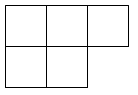 D、
D、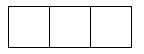 3. 据央视6月初报道,电信5G技术赋能千行百业,打造数字经济底座.5G牌照发放三年来,三大电信运营商共投资4772亿元.把数字4772亿用科学记数法表示为( )A、 B、 C、 D、4. 计算正确的是( )A、 B、 C、 D、5. 小明解方程的步骤如下:
3. 据央视6月初报道,电信5G技术赋能千行百业,打造数字经济底座.5G牌照发放三年来,三大电信运营商共投资4772亿元.把数字4772亿用科学记数法表示为( )A、 B、 C、 D、4. 计算正确的是( )A、 B、 C、 D、5. 小明解方程的步骤如下:解:方程两边同乘6,得①
去括号,得②
移项,得③
合并同类项,得④
以上解题步骤中,开始出错的一步是( )
A、① B、② C、③ D、④6. 在平面直角坐标系中,反比例函数的图象如图所示,则一次函数的图象经过的象限是( ) A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四7. 在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )
A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四7. 在中,用尺规作图,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N.作直线交于点D,交于点E,连接.则下列结论不一定正确的是( )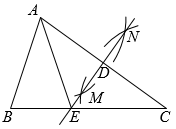 A、 B、 C、 D、8. 在如图所示的纸片中, , D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若 , , 则等于( )
A、 B、 C、 D、8. 在如图所示的纸片中, , D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若 , , 则等于( )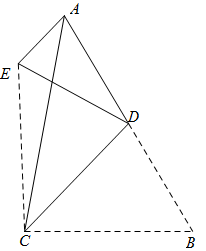 A、 B、 C、 D、9. 某农户承包的36亩水田和30亩旱地需要耕作.每天平均耕作旱地的亩数比耕作水田的亩数多4亩.该农户耕作完旱地所用的时间是耕作完水田所用时间的一半,求平均每天耕作水田的亩数.设平均每天耕作水田x亩,则可以得到的方程为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、 B、 C、 D、9. 某农户承包的36亩水田和30亩旱地需要耕作.每天平均耕作旱地的亩数比耕作水田的亩数多4亩.该农户耕作完旱地所用的时间是耕作完水田所用时间的一半,求平均每天耕作水田的亩数.设平均每天耕作水田x亩,则可以得到的方程为( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 计算:= .12. 已知点 , 在反比例函数的图象上,则与的大小关系是 .13. 如图,在和中, , , , AC与DE相交于点F.若 , 则的度数为 .
 14. 某校九(1)班10名同学进行“引体向上”训练,将他们做的次数进行统计,制成下表:则这10名同学做的次数组成的一组数据中,中位数为 .
14. 某校九(1)班10名同学进行“引体向上”训练,将他们做的次数进行统计,制成下表:则这10名同学做的次数组成的一组数据中,中位数为 .次数
4
5
6
7
8
人数
2
3
2
2
1
15. 已知 , , 则的值为 .16. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .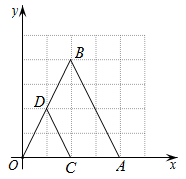 17. 如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的水平距离OA的长是m.
17. 如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的水平距离OA的长是m. 18. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .
18. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .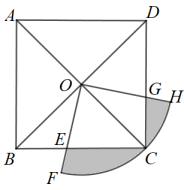 19. 如图,我海军舰艇在某海域C岛附近巡航,计划从A岛向北偏东80°方向的B岛直线行驶.测得C岛在A岛的北偏东50°方向,在B岛的北偏西40°方向.A,B之间的距离为80nmile,则C岛到航线AB的最短距离是nmile.(参考数据: , , 保留整数结果)
19. 如图,我海军舰艇在某海域C岛附近巡航,计划从A岛向北偏东80°方向的B岛直线行驶.测得C岛在A岛的北偏东50°方向,在B岛的北偏西40°方向.A,B之间的距离为80nmile,则C岛到航线AB的最短距离是nmile.(参考数据: , , 保留整数结果) 20. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
20. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .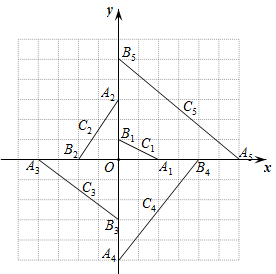
三、解答题
-
21.(1)、计算:;(2)、解不等式组 , 并把解集在数轴上表示出来.
 22. 神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
22. 神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、 ▲ , ▲ ;并补全条形统计图:(2)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;(3)、在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?23. 如图,在中, , 以AB为直径作⊙ , 分别交BC于点D,交AC于点E, , 垂足为H,连接DE并延长交BA的延长线于点F. (1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.24. 某乡镇新打造的“田园风光”景区今年计划改造一片绿化地,种植A、B两种花卉,已知3盆A种花卉和4盆B种花卉的种植费用为330元,4盆A种花卉和3盆B种花卉的种植费用为300元.(1)、每盆A种花卉和每盆B种花卉的种植费用各是多少元?(2)、若该景区今年计划种植A、B两种花卉共400盆,相关资料表明:A、B两种花卉的成活率分别为70%和90%,景区明年要将枯死的花卉补上相同的新花卉,但这两种花卉在明年共补的盆数不多于80盆,应如何安排这两种花卉的种植数量,才能使今年该项的种植费用最低?并求出最低费用.25. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 .
(1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.24. 某乡镇新打造的“田园风光”景区今年计划改造一片绿化地,种植A、B两种花卉,已知3盆A种花卉和4盆B种花卉的种植费用为330元,4盆A种花卉和3盆B种花卉的种植费用为300元.(1)、每盆A种花卉和每盆B种花卉的种植费用各是多少元?(2)、若该景区今年计划种植A、B两种花卉共400盆,相关资料表明:A、B两种花卉的成活率分别为70%和90%,景区明年要将枯死的花卉补上相同的新花卉,但这两种花卉在明年共补的盆数不多于80盆,应如何安排这两种花卉的种植数量,才能使今年该项的种植费用最低?并求出最低费用.25. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 . (1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.26. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
(1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.26. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.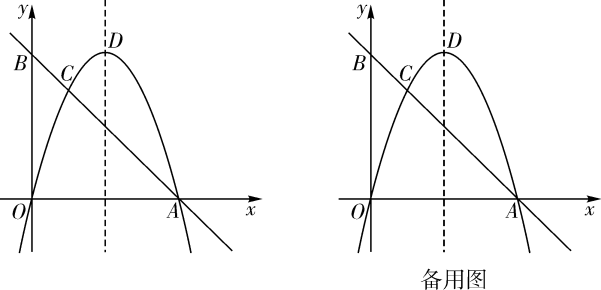 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.