浙江省舟山市定海区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-09 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. 要使代数式 $\sqrt{x - 3}$ 有意义， $x$ 可以取的值为（）

A、4 B、2 C、0 D、-2

查看试题解析
2. 方程 $3 x^{2} = 0$ 的根是（）

A、 $x = 0$ B、 $x_{1} = x_{2} = 0$ C、 $x = 3$ D、 $x_{1} = \sqrt{3} ， x_{2} = - \sqrt{3}$

查看试题解析
3. 如图，图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{4 + 9} = \sqrt{4} + \sqrt{9}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{14} \times \sqrt{7} = 7 \sqrt{2}$ D、 $\sqrt{24} \div \sqrt{3} =$ $2 \sqrt{3}$

查看试题解析
5. 已知点 $A (1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (- 3 ， y_{3})$ 都在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
6. 对于命题“在同一平面内，若 $a / / b$ ， $a / / c$ ，则 $b / / c$ ”，用反证法证明，应假设（）

A、 $a ⊥ c$ B、 $b ⊥ c$ C、 $a$ 与 $c$ 相交 D、 $b$ 与 $c$ 相交

查看试题解析
7. 若一组数据x₁＋1，x₂＋1，…，x_n＋1的平均数为17，方差为2，则另一组数据x₁＋2，x₂＋2，…，x_n＋2的平均数和方差分别为（）

A、17，2 B、18，2 C、17，3 D、18，3

查看试题解析
8. 如图，四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A C ⊥ B D$ ， $E$ ， $F$ 分别是 $A B$ ， $C D$ 的中点，若 $A C = B D = 2$ ，则 $E F$ 的长是（）

A、2 B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\sqrt{2}$

查看试题解析
9. 如图，已知▱ $A B C D$ 的一组邻边 $A B$ ， $B C$ ，用尺规作图作▱ $A B C D$ ，下列4个作图中，作法与理论依据都正确的有几个（）

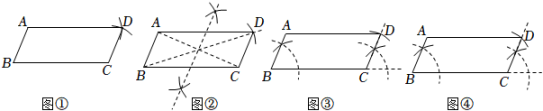A、1个 B、2个 C、3个 D、4个

查看试题解析
10.
如图，矩形ABCD中，AB=4，BC=3，若在AC，AB上各取一点M，N，使BM+MN的值最小，求这个最小值（）

A、 $2 \sqrt{3}$ B、 $\frac{2 \sqrt{119}}{5}$ C、 $2 \sqrt{10}$ D、 $\frac{96}{25}$

查看试题解析

二、填空题（本大题共6小题，共24分）

11. 一组数据－2，3，2，1，－2的中位数为．

查看试题解析
12. 若 $\sqrt{10}$ 的小数部分是 $a$ ，则 $\frac{1}{a + 3}$ 的值是．

查看试题解析
13. 一个多边形的每一个外角都为 $36 °$ ，则这个多边形是边形．

查看试题解析
14. 2020年年收入5万元，预计2022年年收入将达到 $7$ 万元，设2020年到2022年该地区居民年人均收入平均增长率为 $x$ ，可列方程为．

查看试题解析
15. 如图， $A C$ 为四边形 $A B C D$ 的对角线， $∠ A D C = ∠ A C B = 90 °$ ， $A D = C D$ ， $∠ C A B = 30 °$ ， $B C = 2 \sqrt{3}$ ， $E$ ， $F$ 分别是边 $A C$ ， $B C$ 上的动点，当四边形 $D E B F$ 为平行四边形时，该平行四边形的面积是．

查看试题解析
16. 已知函数 $y = x + 1$ 的图象与 $x$ 轴、 $y$ 轴分别交于点 $C$ 、 $B$ ，与双曲线 $y = \frac{k}{x}$ 交于点 $A$ 、 $D .$ 若 $A B + C D = B C$ ，则 $k$ 的值为．

查看试题解析

三、解答题（本大题共8小题，共64分）

17. 化简或计算：

(1)、 $\frac{1}{2} \sqrt{8} - \sqrt{18} + 2 \sqrt{2}$ ；

(2)、 $(\sqrt{3} - 2) \cdot (\sqrt{3} + 2)$ ．

查看试题解析
18. 用配方法解一元二次方程： $2 x^{2} + 3 x + 1 = 0 .$ 小明同学的解题过程如下：

解： $x^{2} + \frac{3}{2} x + \frac{1}{2} = 0$

$x^{2} + \frac{3}{2} x + \frac{9}{4} - \frac{9}{4} + \frac{1}{2} = 0$ ，

$(x + \frac{3}{2})^{2} = \frac{7}{4}$ ，

$x + \frac{3}{2} = \pm \frac{\sqrt{7}}{2}$ ，

$x_{1} = - \frac{3 + \sqrt{7}}{2}$ ， $x_{2} = - \frac{3 - \sqrt{7}}{2}$ ．

小明的解题过程是否正确？若正确，请回答“对”；若错误，请写出你的解题过程．

查看试题解析
19. 如图， $△ A B C$ 中，点 $D$ ， $E$ 分别是边 $A B$ ， $A C$ 的中点，过点 $C$ 作 $C F / / A B$ 交 $D E$ 的延长线于点 $F$ ，连结 $B E$ ．

(1)、求证：四边形 $B C F D$ 是平行四边形．

(2)、当 $A B = B C$ 时，若 $B D = 2$ ， $B E = 3$ ，求 $A C$ 的长．

查看试题解析

20. 某中学九年级组织了一次数学计算比赛（禁用计算器），每班选25名同学参加比赛，成绩分为

A

，

B

，

C

，

D

四个等级，其中

A

等级得分为100分，

B

等级得分为85分，

C

等级得分为75分，

D

等级得分为60分，数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图，请根据提供的信息解答下列问题．

(1)、把一班竞赛成绩统计图补充完整．

(2)、求出下表中

a

，

b

，

c

的值；

	平均数（分）	中位数（分）	众数（分）
一班	$a$	$b$	85
二班	84	75	$C$

(3)、请从以下给出的两个方面对这次比赛成绩的结果进行分析：①从平均数、众数方面来比较一班和二班的成绩；②从

B

级以上（包括

B

级）的人数方面来比较一班和二班的成绩．

查看试题解析

21. 如图，点 $E$ ， $F$ 分别为矩形 $A B C D$ 的边 $A B$ ， $B C$ 的中点，连结 $A F$ ， $D F$ ， $C E$ ， $D E .$ 设 $A F$ 与 $C E$ 交于点 $M$ ．

(1)、找到两对全等三角形（不另添加点与线），并证明其中一对；

(2)、证明： $∠ A M E = ∠ E D F$ ．

查看试题解析
22. 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，减少库存，商场决定采取适当的降价措施．经调查发现，每件衬衫每降价1元，商场平均每天可多售出2件．

(1)、求每件衬衫应降价多少元，能使商场每天盈利1200元；

(2)、小明的观点是：“商场每天的盈利可以达到1300元”，你同意小明的说法吗？若同意，请求出每件衬衫应降价多少元？若不同意，请说明理由．

查看试题解析
23. 背景：点 $A$ 在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上， $A B ⊥ x$ 轴于点 $B$ ， $A C ⊥ y$ 轴于点 $C$ ，分别在射线 $A C$ ， $B O$ 上取点 $D$ ， $E$ ，使得四边形 $A B E D$ 为正方形，如图 $1$ ，点 $A$ 在第一象限内，当 $A C = 4$ 时，小李测得 $C D = 3.5$ ．
探究：通过改变点 $A$ 的位置，小李发现点 $D$ ， $A$ 的横坐标之间存在函数关系．请帮助小李解决下列问题．

(1)、求 $k$ 的值．

(2)、设点 $A$ ， $D$ 的横坐标分别为 $x$ ， $z$ ，将 $z$ 关于 $x$ 的函数称为“ $Z$ 函数”，如图2，小李画出了 $x > 0$ 时“ $Z$ 函数”的图象．
$①$ 求这个“ $Z$ 函数”的表达式．
$②$ 补画 $x < 0$ 时“ $Z$ 函数”的图象，并写出这个函数的性质 $($ 两条即可 $)$ ．

查看试题解析
24. 在正方形 $A B C D$ 中，点 $E$ 在边 $B C$ 上运动，点 $F$ 在边 $D C$ 或 $C B$ 上运动．

(1)、若点 $F$ 在边 $D C$ 上，
$①$ 如图1，已知 $∠ E A F = 45 °$ ，连结 $E F$ ，求证： $E F = B E + D F$ ．
$②$ 如图2，已知 $A E$ 平分 $∠ B A F$ ，求证： $A F = B E + D F$ ．

(2)、若点 $F$ 在边 $C B$ 上，如图 $3$ ，已知 $E$ 为 $B C$ 的中点，且 $∠ D A F = 2 ∠ B A E$ ，求证： $A F = C D + C F$ ．

查看试题解析