浙江省衢州市衢江区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-09 类型:期末考试
一、选择题(本大题共10小题,共30分)
-
1. 的值为( )A、-3 B、3 C、-9 D、92. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、3. 如图,在四边形中, , 与 , 相邻的外角都是 , 则的值为( )
 A、 B、 C、 D、4. 解一元二次方程 , 配方得到 , 则的值为( )A、1 B、-1 C、2 D、-25. 一家鞋店对上周某一品牌的销售情况统计如下表:
A、 B、 C、 D、4. 解一元二次方程 , 配方得到 , 则的值为( )A、1 B、-1 C、2 D、-25. 一家鞋店对上周某一品牌的销售情况统计如下表:尺码厘米
22.5
23
23.5
24
24.5
销售量双
2
5
11
7
3
该店决定本周进鞋时多进些尺码为23.5厘米的鞋,影响鞋店决策的统计量是( )
A、平均数 B、中位数 C、众数 D、方差6. 用反证法证明“四边形中至少有一个角是钝角或直角”,可假设四边形的四个角都是( )A、钝角或直角 B、钝角 C、直角 D、锐角7. 如图,在平行四边形中,是对角线 , 的交点.已知 , , 的周长是11则对角线的长为( ) A、3 B、4 C、5 D、68. 某景点的门票价格为220元,日接待游客5000人.当门票价格每提高10元,日游客数减少50人.若想每天的门票收入达到138万元,问门票价格需提高多少元?设门票价格提高元,则可列方程为( )A、 B、 C、 D、9. 如图,用直尺和圆规在矩形内进行构图:以为圆心,长为半径作弧交于点 , 连结 , 再以为圆心,长为半径作弧交于点 , 连结下列结论不一定成立的是( )
A、3 B、4 C、5 D、68. 某景点的门票价格为220元,日接待游客5000人.当门票价格每提高10元,日游客数减少50人.若想每天的门票收入达到138万元,问门票价格需提高多少元?设门票价格提高元,则可列方程为( )A、 B、 C、 D、9. 如图,用直尺和圆规在矩形内进行构图:以为圆心,长为半径作弧交于点 , 连结 , 再以为圆心,长为半径作弧交于点 , 连结下列结论不一定成立的是( ) A、 B、 C、 D、10. 如图,在反比例函数的图象上有点 , , , 它们的横坐标依次为1,3,6,分别过这些点作轴与轴的垂线段.图中阴影部分的面积记为 , 若 , 则的值为( )
A、 B、 C、 D、10. 如图,在反比例函数的图象上有点 , , , 它们的横坐标依次为1,3,6,分别过这些点作轴与轴的垂线段.图中阴影部分的面积记为 , 若 , 则的值为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(本大题共6小题,共18分)
-
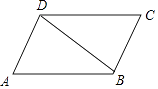
11. 设实数的整数部分为 , 则 .12. 已知关于的一元二次方程的一个根2,则 .13. 如图,在▱ABCD中,∠A=70°,DC=DB,则∠CDB= .
 14. 如图是我市某天早上和晚上各四个整点时的气温折线统计图.请根据统计图判断该天早上和晚上的气温更稳定的是.(填“早上”“晚上”).
14. 如图是我市某天早上和晚上各四个整点时的气温折线统计图.请根据统计图判断该天早上和晚上的气温更稳定的是.(填“早上”“晚上”). 15. 如图是函数和函数在第一象限部分的图象,则时,使成立的的取值范围是 .
15. 如图是函数和函数在第一象限部分的图象,则时,使成立的的取值范围是 . 16. 如图所示,将一张直角三角形纸片ABC剪成①二③④四部分,恰好拼成一个无缝隙无重叠的正方形.已知∠ACB=90°,AC=6,BC=8,则:
16. 如图所示,将一张直角三角形纸片ABC剪成①二③④四部分,恰好拼成一个无缝隙无重叠的正方形.已知∠ACB=90°,AC=6,BC=8,则: (1)、DE= .(2)、GF= .
(1)、DE= .(2)、GF= .三、解答题(本大题共7小题,共52分)
-
17. 计算:(1)、 .(2)、 .18. 解方程:(1)、 .(2)、 .19. 北京冬奥会女子大跳台决赛的打分规则;6名裁判打分,去除一个最高分和一个最低分,剩余4个分数的平均值为该选手成绩.下表是中国选手谷爱凌第一跳的得分情况,其中裁判4,裁判5的打分(分别为94分和分)被去除.
裁判1
裁判2
裁判3
裁判4
裁判5
裁判6
裁判7
94分
94分
94分
94分
分
分
93.75分
请根据表中信息,解决以下问题;
(1)、求的值.(2)、判断是否最低分并说明理由.(3)、从平均数的特征说说打分规则中去除一个最高分及一个最低分的合理性.20. 如图,点 , 分别是平行四边形的边 , 上的点,且 .求证: .
 21. 如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示:
21. 如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示:
桌面所受压强
400
500
800
1000
1250
受力面积
0.5
0.4
0.2
0.16
 (1)、根据表中数据,求出压强关于受力面积的函数表达式及的值.(2)、如图2,将另一长,宽,高分别为 , , , 且与原长方体相同重量的长方体放置于该水平玻璃桌面上.若玻璃桌面能承受的最大压强为 , 问:这种摆放方式是否安全?请判断并说明理由.22. 某农家购买了一卷由边长为的小菱形构成的网格防护网(如图1)用于“未来乡村”建设.
(1)、根据表中数据,求出压强关于受力面积的函数表达式及的值.(2)、如图2,将另一长,宽,高分别为 , , , 且与原长方体相同重量的长方体放置于该水平玻璃桌面上.若玻璃桌面能承受的最大压强为 , 问:这种摆放方式是否安全?请判断并说明理由.22. 某农家购买了一卷由边长为的小菱形构成的网格防护网(如图1)用于“未来乡村”建设. (1)、该农家计划利用已有的一堵长为8米的墙,用该种防护网围成一个面积为的矩形园子ABCD(如图2).若防护网用去24米,求矩形一边的长度.(2)、如图3,边长为的小菱形中,:: , 防护网高度为问:24米防护网中最多有几个这样的小菱形?(注:防护网在转角处不被裁断).23. 如图1,已知正方形与等腰 , , 点 , 分别在 , 边上滑动,点在正方形内.
(1)、该农家计划利用已有的一堵长为8米的墙,用该种防护网围成一个面积为的矩形园子ABCD(如图2).若防护网用去24米,求矩形一边的长度.(2)、如图3,边长为的小菱形中,:: , 防护网高度为问:24米防护网中最多有几个这样的小菱形?(注:防护网在转角处不被裁断).23. 如图1,已知正方形与等腰 , , 点 , 分别在 , 边上滑动,点在正方形内. (1)、求证:点到 , 的距离相等.(2)、若 , .
(1)、求证:点到 , 的距离相等.(2)、若 , .如图2,当点为边的中点时,求的长度.
求在整个滑动过程中长度的取值范围.