浙江省衢州市开化县2021-2022学年九年级上学期第一次调研检测数学试卷
试卷更新日期:2022-08-09 类型:月考试卷
一、单选题
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点P在半径为8的外,则( )A、 B、 C、 D、3. 2021年开化县创建全国文明城市,特别注重垃圾分类.垃圾分类的英文“garbage sorting”,从中随机抽取一个字母,抽中字母是a的概率是( )A、 B、 C、 D、4. 以下列数据(单位:cm)为长度的各组线段中,成比例线段的是( )A、1,2,3,4 B、3,6,9,18 C、1,2,2,6 D、1, , 4,35. 若 , 则等于( )A、 B、 C、 D、6. 如图,在中, , , , 则的长为( )
2. 已知点P在半径为8的外,则( )A、 B、 C、 D、3. 2021年开化县创建全国文明城市,特别注重垃圾分类.垃圾分类的英文“garbage sorting”,从中随机抽取一个字母,抽中字母是a的概率是( )A、 B、 C、 D、4. 以下列数据(单位:cm)为长度的各组线段中,成比例线段的是( )A、1,2,3,4 B、3,6,9,18 C、1,2,2,6 D、1, , 4,35. 若 , 则等于( )A、 B、 C、 D、6. 如图,在中, , , , 则的长为( ) A、2 B、3 C、4 D、57. 在平面直角坐标系中,把抛物线先向下平移3个单位长度再向右平移2个单位长度,所得到的抛物线的解析式为( )A、 B、 C、 D、8. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②;③当时,y随x增大而增大.其中结论正确的个数为( )
A、2 B、3 C、4 D、57. 在平面直角坐标系中,把抛物线先向下平移3个单位长度再向右平移2个单位长度,所得到的抛物线的解析式为( )A、 B、 C、 D、8. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②;③当时,y随x增大而增大.其中结论正确的个数为( ) A、0个 B、1个 C、2个 D、3个9. 如图,一块含30°角的三角板和一块量角器,点O为EF的中点,AC经过点O,AC=EF,∠FOC=120°,AC=4,点B恰在弧ECF上,则图中阴影部分的面积为( )
A、0个 B、1个 C、2个 D、3个9. 如图,一块含30°角的三角板和一块量角器,点O为EF的中点,AC经过点O,AC=EF,∠FOC=120°,AC=4,点B恰在弧ECF上,则图中阴影部分的面积为( ) A、 B、 C、 D、10. 我们将顶角为36°的等腰三角形称为黄金三角形(底边和腰的比值为黄金分割比).如图,已知 , 为第一个黄金三角形,为第二个黄金三角形,…,依次类推则第2021个黄金三角形的底边长为( )
A、 B、 C、 D、10. 我们将顶角为36°的等腰三角形称为黄金三角形(底边和腰的比值为黄金分割比).如图,已知 , 为第一个黄金三角形,为第二个黄金三角形,…,依次类推则第2021个黄金三角形的底边长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 抛物线的开口方向是 . (选填“向上”或“向下”)12. 在一张比例尺为的地图上,A、B两地间的图上距离为3厘米,则两地间的实际距离是千米.13. 对一批口罩进行抽检,统计合格口罩的只数,得到合格口罩的频率如下:
抽取只数(只)
10
50
100
300
800
1800
3000
5000
合格频率
0.90
0.92
0.91
0.91
0.90
0.90
0.90
0.90
某校购进该批次口罩共20000只,则合格的有只.
14. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为m. 15. 如图,矩形中, , , 点P从点A出发,沿边向点B以1cm/s的速度移动;点Q从点B出发,沿边向点C以2cm/s的速度移动.P,Q同时出发,分别到B,C后停止移动,则的最小面积是 .
15. 如图,矩形中, , , 点P从点A出发,沿边向点B以1cm/s的速度移动;点Q从点B出发,沿边向点C以2cm/s的速度移动.P,Q同时出发,分别到B,C后停止移动,则的最小面积是 . 16. 如图,是半径为6的半圆O的直径,点C是直径上的动点,过点C做交半圆O于点D.以 , 为边分别向左,向下作等边和等边 , 连结 . 设和的面积分别为和
16. 如图,是半径为6的半圆O的直径,点C是直径上的动点,过点C做交半圆O于点D.以 , 为边分别向左,向下作等边和等边 , 连结 . 设和的面积分别为和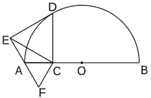 (1)、当时, .(2)、当时,则 .
(1)、当时, .(2)、当时,则 .三、解答题
-
17. 已知线段a,b的比例中项线段 , 线段 , 求线段b.18. “绿色出行一小步,健康环保一大步”.为了提倡低碳出行(低碳出行:公交、骑车、步行等)人人参与,现需要招募三支自愿者宣传队,分别是A公交文明队,B骑行宣传队和C步行达人队.小明和小红都想报名参加,每人只能选其中一支自愿者队参加活动,求两人参加同时报名参加骑行宣传队的概率.(画树状图或列表求解)19. 为了开展项目化学习,小亮同学用自制的直角三角形纸板测量一颗树的高度.他调整自己的位置,设法使斜边保持水平,并且边与树顶B在同一直线上.已知纸板的两条边 , , 延长交于点C,测得边离地面的高度 , , 求树高的长.
 20. 如图,在的正方形网格图中,小正方形的边长都为1,的顶点都在格点上,在该网格图中只用无刻度的直尺作图,保留作图痕迹.
20. 如图,在的正方形网格图中,小正方形的边长都为1,的顶点都在格点上,在该网格图中只用无刻度的直尺作图,保留作图痕迹.
( 1 )画出的外接圆圆心O.
( 2 )连结 , , 求的长.
21. 现有一个文具袋,如图1所示,文具袋的上部分可以看成一个二次函数图象,下部分是矩形,文具袋的最大高度是13.5cm,底边长是22cm,矩形的宽是8cm.如图2,建立平面直角坐标系. (1)、求出该二次函数的表达式.(2)、某笔记本如图3的长和宽分别是20cm和10cm,试判断笔记本能不能放入文件袋中,请说明理由.22. 如图,在△ABC中,点D在BC上,连结AD,把△ADC沿着AD折叠得到△ADC′,交BC边于E,若DC′∥AB.
(1)、求出该二次函数的表达式.(2)、某笔记本如图3的长和宽分别是20cm和10cm,试判断笔记本能不能放入文件袋中,请说明理由.22. 如图,在△ABC中,点D在BC上,连结AD,把△ADC沿着AD折叠得到△ADC′,交BC边于E,若DC′∥AB. (1)、求证: .(2)、若 , , 求的值及的长.23. 定义:关于x轴对称且对称轴相同的两条抛物线叫作“镜像抛物线”.
(1)、求证: .(2)、若 , , 求的值及的长.23. 定义:关于x轴对称且对称轴相同的两条抛物线叫作“镜像抛物线”.例如:的“镜像抛物线”为 .
 (1)、请写出抛物线的顶点坐标 , 及其“镜像抛物线的顶点坐标 . 写出抛物线的“镜像抛物线”为 .(2)、如图,在平面直角坐标系中,点B是抛物线上一点,点B的横坐标为1,过点B作x轴的垂线,交抛物线L的“镜像抛物线”于点C,分别作点B,C关于抛物线对称轴对称的点 , , 连接 , , , .
(1)、请写出抛物线的顶点坐标 , 及其“镜像抛物线的顶点坐标 . 写出抛物线的“镜像抛物线”为 .(2)、如图,在平面直角坐标系中,点B是抛物线上一点,点B的横坐标为1,过点B作x轴的垂线,交抛物线L的“镜像抛物线”于点C,分别作点B,C关于抛物线对称轴对称的点 , , 连接 , , , .①当四边形为正方形时,求a的值.
②求正方形所含(包括边界)整点个数.(说明:整点是横、纵坐标均为整数的点)
24. 如图,在中, , D是上的一点,E是射线上一动点,连接 , 过点A作的平行线交延长线于点F,已知 , .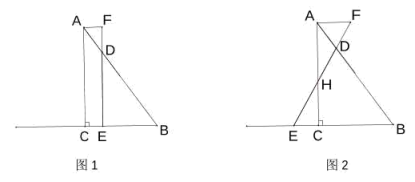 (1)、当时,
(1)、当时,①如图1,若 , 求的长.
②如图2,与相交于H点,若 , 求的值.
(2)、当时,若与相似,求的值.(直接写出答案)