江苏省镇江市丹徒区2021-2022学年九年级上学期第一次月考数学试卷

试卷更新日期：2022-08-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中是关于x的一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $x^{2} + 5 x = x^{2} + 1$ C、 $4 x^{2} - 6 x = 7$ D、 $2 x^{3} - x - 5 = 0$

查看试题解析
2. 一元二次方程 $y^{2} - y - \frac{3}{4} = 0$ 配方后可化为（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = 1$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
3. 关于x的一元二次方程 $(a - 1) x^{2} + x + | a | - 1 = 0$ 的一个根为0，则实数a的值为（）

A、-1 B、0 C、1 D、-1或1

查看试题解析
4. 判断一元二次方程 $x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
5. 一个等腰三角形的两条边长分别是方程2x²﹣13x+15＝0的两根，则该等腰三角形的周长是（　　）

A、8 B、11.5 C、10 D、8或11.5

查看试题解析
6. 已知a是方程x²+x﹣1=0的一个根，则 $\frac{2}{a^{2} - 1} - \frac{1}{a^{2} - a}$ 的值为（　　）

A、 $\frac{- 1 + \sqrt{5}}{2}$ B、 $\frac{- 1 \pm \sqrt{5}}{2}$ C、﹣1 D、1

查看试题解析

二、填空题

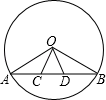
7. 若方程 $x^{k - 1}$ -2x-3=0是关于x的一元二次方程，则k= ．

查看试题解析
8. 一元二次方程 $(1 + 3 x) (x - 3) = 2 x^{2} + 1$ 化为一般形式为．

查看试题解析
9. 方程4（x﹣1）²＝1的根是．

查看试题解析
10. 如图，AB是⊙O的直径，点D，C在⊙O上，AD∥OC，∠DAB＝60°，连接AC，则∠DAC的度数为．

查看试题解析
11. 已知一元二次方程x²-6x+5-k=0的根的判别式△=4，则k= ．

查看试题解析
12. 已知x₁ ， x₂是一元二次方程x²﹣2x﹣1=0的两根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ =

查看试题解析
13. 若一元二次方程x²﹣x+k=0有实数根，则k的取值范围是．

查看试题解析
14. 一元二次方程x²+3﹣2 $\sqrt{3}$ x=0的解是．

查看试题解析
15. 两个连续整数的平方和为113，则这两个连续整数为．

查看试题解析
16. 某品牌的手机经过四、五月份连续两次降价，每部售价由2500元降到了1600元，则平均每月降价的百分率是.

查看试题解析
17. 关于x的方程a（x+m）²+b=0的根是x₁=4，x₂=-6，（a，b，m均为常数，a≠0），则关于x的方程a（x+m-3）²+b=0的根是．

查看试题解析
18. 已知x为实数，且满足（x+1）（x+2）（x+3）（x+4）=48，则x²+5x= ．

查看试题解析

三、解答题

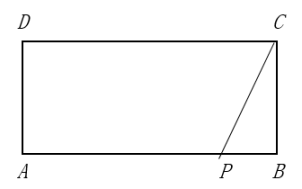
19. 用适当的方法解下列方程

(1)、x $^{2}$ ＝3

(2)、 $x^{2} - 4 x - 96 = 0$

(3)、x（2x－4）＝6－8x

(4)、2x $^{2}$ －8x－1＝0

查看试题解析
20. 已知：如图，在⊙O中，AB为弦，C、D两点在AB上，且AC＝BD．求证： $△ O A C ≌ △ O B D$ ．

查看试题解析
21. 已知关于x的方程 $x^{2} - 6 x + m^{2} - 3 m - 5 = 0$ 的一个根为一1，求另一个根及m的值.

查看试题解析
22. 已知一元二次方程ax²+bx+c＝0的一个根为1，且a、b满足b＝ $\sqrt{a - 2} + \sqrt{2 - a}$ +3，求c的值．

查看试题解析
23. 已知关于x的一元二次方程x²﹣4x﹣m²＝0．

(1)、求证：该方程有两个不相等的实数根；

(2)、若该方程的两个实数根x₁ ， x₂满足 $x_{1} x_{2} + x_{1} + x_{2} ＝ 3$ ，求m的值．

查看试题解析
24. 某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件；

(1)、若商场平均每天要赢利1200元，每件衬衫应降价多少元？

(2)、每件衬衫降价多少元时，商场平均每天赢利最多？

查看试题解析
25. 矩形ABCD中，AB=17，BC= $\sqrt{21}$ ，点P在AB边上，且满足AP=3PC，求PB之长．

查看试题解析
26. 已知CD为△ABC的中线，∠A及∠BDC的度数分别是方程x²-75x+1350=0的两根，

(1)、求∠A及∠BDC的度数；

(2)、求∠B的度数．

查看试题解析