江苏省宜兴市丁蜀学区2021-2022学年九年级上学期第一次质量调研考试数学试卷

试卷更新日期：2022-08-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，是关于x的一元二次方程的是（）

A、 ${(x + 1)}^{2} = 2 (x + 1)$ B、 $\frac{1}{x^{2}} + \frac{1}{x} - 2 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $x^{2} - 2 x = x^{2}$

查看试题解析
2. 已知一元一次方程 $x^{2} + x - 1 = 0$ ，下列判断正确的是（）

A、该方程有两个相等的实数根 B、该方程有两个不相等的实数根 C、该方程无实数根 D、该方程根的情况不确定

查看试题解析
3. 用配方法解一元二次方程x² - 6x + 5 = 0，其中配方正确的是（　　）

A、（x - 3）² = 5 B、（x – 3）² = -4 C、（x - 3）² = 4 D、（x - 3）² = 9

查看试题解析
4. 一元二次方程（x﹣2）²=9的两个根分别是（）

A、x₁=1，x₂=﹣5 B、x₁=﹣1，x₂=﹣5 C、x₁=1，x₂=5 D、x₁=﹣1，x₂=5

查看试题解析
5. 三角形两边的长是3和4，第三边的长是方程 $x^{2} - 12 x + 35 = 0$ 的根，则该三角形的周长为（）

A、14 B、12 C、12或14 D、以上都不对

查看试题解析
6. 电视节目主持人在主持节目时，站在舞台黄金分割点处最自然得体，若舞台AB长20m，试计算主持人应走到离A至少多少米处是比较得体的位置?(A在B左边，主持人在A处) （）

A、7.64m B、12.3m C、13.4 m D、6m

查看试题解析
7. 关于x的一元二次方程（m﹣1）x²+5x+m²﹣3m+2=0，常数项为0，则m值等于（）

A、1 B、2 C、1或2 D、0

查看试题解析
8. 已知α，β是方程 $x^{2} + 2015 x + 1 = 0$ 的两个根，则 $(α {}^{2}+ 2016 α + 1) (β {}^{2}+ 2016 β + 1)$ 的值（）

A、1 B、2 C、3 D、4

查看试题解析
9. 若x₁+x₂=3，x₁²+x₂²=5，则以x₁、x₂为根的一元二次方程是（）

A、x²-3x+2=0 B、x²+3x-2=0 C、x²+3x+2=0 D、x²-3x-2=0

查看试题解析
10. 给出一种运算：对于函数y=xⁿ ，规定 $y^{'}$ =nx^n-1 ．例如：若函数y₁=x⁴ ，则有 $y^{'} = 4 x^{3}$ ．函数y=x³ ，则方程 $y^{'} = 12$ 的解是（）

A、x₁=4，x₂=-4 B、x₁=2 $\sqrt{3}$ ，x₂=-2 $\sqrt{3}$ C、x₁=x₂=0 D、x₁=2，x₂=-2

查看试题解析

二、填空题

11. 一元二次方程 $3 x^{2} - 2 x - 5 = 0$ 的一次项系数是．

查看试题解析
12. 若x=2是方程x²+3x﹣2m=0的一个根，则m的值为．

查看试题解析
13. 已知关于x的方程 $(m - 1) x^{| m | + 1} + (2 m + 1) x - m = 0$ 是一元二次方程，则 $b + c =$ ．

查看试题解析
14. 已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4} \neq 0$ ，则 $\frac{x^{2} + x y}{y z} =$

查看试题解析
15. 现定义运算“★”，对于任意实数a、b，都有a★b=a²﹣3a+b，如：3★5=3²﹣3×3+5，若x★2=6，则实数x的值是．

查看试题解析
16. A、B两地的距离AB=5km，在图上量得对应的距离A’B’=2cm，则图上距离与实际距离之比为．

查看试题解析
17. 某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则一株的盈利为元，可列出的方程是．

查看试题解析
18. 已知关于x的方程a(x+c)²+b=0(a，b，c为常数，a≠0)的两根分别为-2，1，那么关于x的方程a(x+c-2)²+b=0的两根分别为， c= ．

查看试题解析

三、解答题

19. 解方程

(1)、 $3 x^{2} = 12$

(2)、 $2 x^{2} - 3 x = 0$

(3)、 $2 x^{2} + 3 x - 1 = 0$

(4)、（2x﹣1）²﹣x²=0

(5)、 $x^{2} - 4 x - 12 = 0$

(6)、 $(2 x - 1)^{2} - 2 x + 1 = 0$

查看试题解析
20. 已知：如图， $A C$ ， $D B$ 相交于点O， $A B = D C$ ， $∠ A B O = ∠ D C O$ .

求证：

(1)、 $△ A B O ≌ △ D C O$

(2)、 $∠ O B C = ∠ O C B$ .

查看试题解析
21. 如果 $x^{2} + y^{2} - 10 x - 16 y + 89 = 0$ ，求 $\frac{x}{y}$ 的值．

查看试题解析
22. 当x取何值时，代数式2x²-6x+7的值最小？并求出这个最小值．

查看试题解析
23. 已知关于x的方程 $\frac{1}{4} x^{2} - (m - 2) x + m^{2} = 0$ 有两个不相等的实数根x₁ ， x₂ ．

(1)、求m的取值范围；

(2)、是否存在实数m，使方程的两个实数根互为相反数？如果存在，求出m的值；如果不存在，说明理由．

查看试题解析
24. 已知关于x的方程 $\frac{1}{4} x^{2} - (m - 2) x + m^{2} = 0$ 是否存在正数m，使方程的两个实数根的平方和等于224？若存在，求出满足条件的m的值．

查看试题解析
25. 如图，△ADE∽△ABC，AD＝3cm，AE＝2cm，CE＝4cm，BC＝9cm

(1)、求BD、DE的长；

(2)、求△ADE与△ABC的周长比．

查看试题解析
26. 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：每千克核桃应降价多少元？

查看试题解析
27. 关于x的一元二次方程 $(a + c) x^{2} - 2 b x + (a - c) = 0$ ，其中a，b，c分别为 $△ A B C$ 三边长．

(1)、若方程有两个相等的实数根，试判断 $△ A B C$ 的形状，并说明理由；

(2)、若 $△ A B C$ 是等边三角形，试求这个一元二次方程的根．

查看试题解析
28. 如图，在Rt△ABC中，∠B=90°，BC=5 $\sqrt{3}$ ，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．

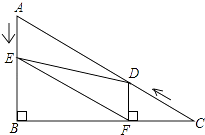(1)、求证：AE=DF；

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析