江苏省盐城市亭湖区2021-2022学年九年级上学期10月月考数学试卷
试卷更新日期：2022-08-09 类型：月考试卷
一、单选题
-
1. 某运动品牌经销商对鞋码大小进行抽样调查，经销商最感兴趣的数据是（ ）A、中位数 B、平均数 C、众数 D、方差2. 一元二次方程的根的情况为（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. ⊙O的半径为4，圆心到直线的l的距离为3，则直线l与⊙O的位置关系是（ ）A、相离 B、相切 C、相交 D、相切或相交4. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根，则实数m的取值范围是（ ）A、m≥1 B、m≤1 C、m＞1 D、m＜15. 如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC的度数是 （ ）
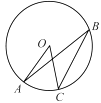A、25° B、65° C、50° D、130°6. 如图，在中， ， ， 以点C为圆心，BC为半径的圆分别交AB、AC于点D、点E，则弧BD的度数为
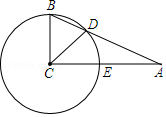A、 B、 C、 D、7. 下列命题中，正确的个数是（ ）(1)、三点确定一个圆；（2）等弧所对的圆周角相等；（3）相等的圆心角所对的弧相等；（4）直径所对的圆周角是直角．A、1个 B、2个 C、3个 D、4个8. 到三角形三条边的距离相等的点是三角形（ ）的交点.A、三条中线 B、三条角平分线 C、三条高 D、三条边的垂直平分线二、填空题
-
9. 方程x2 -7=0的根是 ．10. 已知一组数据：-1，0，1，2，3，则这组数据的方差是.11. 一组数据23，27，18，21，12的中位数是 ．12. 某企业2010年底缴税40万元，2012年底缴税48.4万元，设这两年该企业缴税的年平均增长率为x，根据题意，可得方程 ．13. 已知方程的两个实数根分别为m，n，则的值为14. 底面半径为4cm，母线长为6cm的圆锥的侧面积为 ．15. 矩形ABCD中，边AB＝6cm，AD＝8cm，以A为圆心作⊙A，使B、C、D三点有两个点在⊙A内有一点在⊙A外，则⊙A的半径r的取值范围是 ．
16. 如图，点I为△ABC的内心，连AI交△ABC的外接圆于点D，若 ， 点E为弦AC的中点，连接EI，IC，若 ， ， 则IE的长为 ．
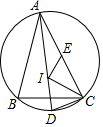
三、解答题
-
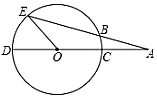
17. 解下列方程(1)、2x2－5x－1＝0；(2)、(x +2)2＝3x +6.18. 已知关于x的一元二次方程x2﹣（m+2）x+2m＝0．(1)、求证：不论m为何值，该方程总有两个实数根；(2)、若直角△ABC的两直角边AB、AC的长是该方程的两个实数根，斜边BC的长为3，求m的值．19. 如图，CD是圆O的直径，点A在DC的延长线上，∠EOD＝84°，AE交圆O于点B，且AB＝OC．求∠A的度数．
20. 某篮球队对队员进行定点投篮测试，每人每次投篮10次，现对甲、乙两名队员在五次中进球数（单位：个）进行统计，结果如表：第1次
第2次
第3次
第4次
第5次
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2.
(1)、求乙进球的平均数和方差；(2)、如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？21. 如图，在平面直角坐标系xOy中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0）．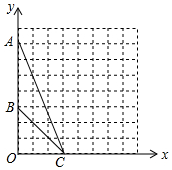
(1)、在图中利用直尺画出△ABC的外接圆的圆心点D，圆心D的坐标为 ；(2)、求△ABC外接圆的面积；(3)、若点E的坐标（6，0），点E在△ABC外接圆（填“圆内”“圆上“或“圆外”）22. 如图在Rt△ABC中，∠C=90°，BD平分∠ABC，过D作DE⊥BD交AB于点E，经过B，D，E三点作⊙O．
(1)、求证：AC与⊙O相切于D点；(2)、若AD=15，AE=9，求⊙O的半径．23. 如图，在△ABC中，经过A，B两点的⊙O与边BC交于点E，圆心O在BC上，过点O作OD⊥BC交⊙O于点D，连接AD交BC于点F，且AC＝FC．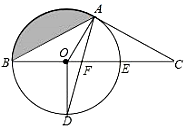
(1)、试判断AC与⊙O的位置关系，并说明理由；(2)、若FC＝ ， CE＝1．求图中阴影部分的面积（结果保留π）．24. 已知，如图，扇形AOB的圆心角为120°，半径OA为6cm.
(1)、求扇形AOB的弧长和扇形面积；(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒，求这个纸盒的高OH.25. 某超市将进价为160元的商品按每件200元出售，每天可销售100件．为了尽可能的让利于顾客，超市决定采取适当的降价措施．经市场调查，发现这种商品每降价2元，其销售量就增加10件．设后来该商品每件降价x元．(1)、超市经营该商品，原来一天可获利润元；(2)、若超市经营该商品一天要获利润4320元，则每件商品应降价多少元？26.
(1)、学习心得：小刚同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．例如：已知，如图1，在ABC中，AB＝AC，∠BAC＝90°，D是ABC外一点，且AD＝AC，求∠BDC的度数．若以点A为圆心，AB为半径作辅助圆⊙A，则点C、D必在⊙A上，∠BAC是⊙A的圆心角，而∠BDC是圆周角，从而可容易得到∠BDC＝ ． （直接写答案）(2)、问题解决：如图2，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠BDC＝25°，求∠BAC的度数；(3)、问题拓展：如图3，在ABC中，∠BAC＝45°，AD是BC边上的高，且BD＝4，CD＝2，求AD的长．27. 【概念认识】自一点引出的两条射线分别经过已知线段的两端，则这两条射线所成的角称为该点对已知线段的视角，如图①，∠APB是点P对线段AB的视角．数学理解，如图②，已知线段AB与直线l，在直线l上取一点P，使点P对线段AB的视角最大．
(1)、过A、B两点，作⊙O使其与直线相切，切点为P，则点P对线段AB的视角最大，即∠APB最大，为了证明点P的位置即为所求，不妨在直线l上另外任取一点Q，连接AQ，BQ，证明：∠APB＞∠AQB即可，请完成这个证明．(2)、【问题解决】在足球电子游戏中，足球队球门的视角越大，越容易被踢进，如果一名球员沿直线带球前进，那么他应当在哪个地方射门，才能使进球的可能性最大？
如图③，A、B是足球门的两端，线段AB是球门的宽，CD是球场边线，∠ADC是直角．①若该球员沿边线CD带球前进，记足球所在的位置为点P，在图③中，用直尺和圆规在线段CD上求作点P，使点P对AB的视角最大（不写作法，保留作图痕迹）．
②若M是线段CD上一点，∠CMN＝60°，该球员沿射线MN带球前进（如图④），记足球所在的位置为点P，已知AB＝4，BD＝9，DM＝ ， 求点P对AB的最大视角.