江苏省盐城市东台市二联盟2021-2022学年九年级上学期第一次阶段测试数学试卷

试卷更新日期：2022-08-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 方程 $(x + 0.5) (x - 2) = 0$ 的根为（　　）

A、 $x_{1} = 2$ ， $x_{2} = - 0.5$ B、 $x_{1} = - 2$ ， $x_{2} = 0.5$ C、 $x_{1} = 2$ ， $x_{2} = 0.5$ D、 $x_{1} = - 2$ ， $x_{2} = - 0.5$

查看试题解析
2. 下列说法正确的是（）

A、形如ax²＋bx＋c＝0的方程叫做一元二次方程 B、(x＋1)(x－1)＝0是一元二次方程 C、方程x²－2x＝1的常数项为0 D、一元二次方程中，二次项系数、一次项系数及常数项都不能为0

查看试题解析
3. 一个等腰三角形的两条边长分别是方程 $x^{2} - 7 x + 10 = 0$ 的两根，则该等腰三角形的周长是（）

A、12 B、9 C、13 D、12或9

查看试题解析
4. 某饲料厂今年一月份生产饲料 $500$ 吨，三月份生产饲料 $720$ 吨，若二月份和三月份这两个月平均增长率为x，则有（）.

A、 $500 (1 + 2 x) = 720$ B、 $500 (1 + x^{2}) = 720$ C、 $500 {(1 + x)}^{2} = 720$ D、 $720 {(1 + x)}^{2} = 500$

查看试题解析
5. 如图，A，B，C是 $⊙ O$ 上的三点， $∠ B A C = 50 °$ ，则 $∠ B O C$ 的度数为（）

A、100° B、110° C、125° D、130°

查看试题解析
6. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于（）

A、20° B、30° C、40° D、50°

查看试题解析
7. 如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段OM的长的取值范围是（）

A、 $3 \leq O M \leq 5$ B、 $4 \leq O M \leq 5$ C、 $3 < O M < 5$ D、 $4 < O M < 5$

查看试题解析
8. 如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M ，连接OP ， OM ．若⊙O的半径为2，OP=4，则线段OM的最小值是（　　）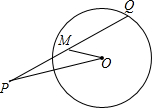

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 方程 $x^{2} - 2 = 0$ 的解为

查看试题解析
10. 关于x的方程 $(a - 1) x^{1 + a^{2}} = 1$ 是一元二次方程，则a的值是

查看试题解析
11. 一个直角三角形的两条边长是方程 $x^{2} - 7 x + 12 = 0$ 的两个根，则此直角三角形的外接圆的直径为．

查看试题解析
12. 已知m，n是方程x²+4x﹣5=0的两个实数根，则m﹣mn+n= ．

查看试题解析
13. 已知一点到圆周上点的最大距离为 $9$ ，最短距离为 $1$ ，则圆的直径为.

查看试题解析
14. 如图，在△ABC中，∠C=90°，AC=8，BC=6，内切圆⊙O分别切边AC、BC于点D、E，则其内切圆的半径r等于．

查看试题解析
15. ⊙O的半径为R ，点O到直线l的距离为d ， R ， d是方程 x² -4x+m=0的两根，当直线l与⊙O相切时，m的值为．

查看试题解析
16. 如图，在⊙O中， $\overset{⌢}{A B} = \overset{⌢}{C D}$ ， A、C之间的距离为4，则线段BD＝．

查看试题解析
17.
如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是．

查看试题解析
18. 如图，在Rt△ABC中， $∠ A B C = 90 °$ ， $B C = 2$ ，点D在AC边上运动，将△BCD沿BD对折，点C的对应点是 $C'$ ，在点D从C到点A的运动过程中，点 $C'$ 运动的路径长．

查看试题解析

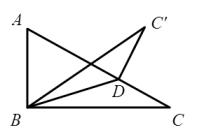
三、解答题

19. 解方程

(1)、 $x^{2} - 2 x - 4 = 0$

(2)、x²-2x-3=0(配方法)

查看试题解析
20. 如果关于x的方程 $k x^{2} - 3 x + 1 = 0$ 有实数根，试求k的取值范围

查看试题解析
21. 服装柜在销售中发现某品牌童装平均每天可售出20件，每件盈利40元.为了迎接“六一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存.经市场调查发现，如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？

查看试题解析
22. 已知⊙O的直径为10，AB、CD是两条平行的弦，且AB＝6、CD＝8，求AB、CD之间的距离

查看试题解析
23. 如图，⊙O的半径OC⊥AB，D为 $\overset{⌢}{B C}$ 上一点，DE⊥OC，DF⊥AB，垂足分别为E、F，EF=3，求直径AB的长．

查看试题解析
24. 如图， $A B$ 是半圆的直径，O是圆心，C是半圆上一点，D是弧 $A C$ 的中点， $O D$ 交弦 $A C$ 于E，若 $A C = 8$ ， $D E = 2$ .

(1)、求 $O D$ 的长度；

(2)、连接 $B E$ ，求 $B E$ 的长度.

查看试题解析
25. 如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OD⊥AB于点O，分别交AC、CF于点E、D，且CF是⊙O的切线．

(1)、求证：DE=DC；

(2)、若⊙O的半径为5，OE=1，求DE的长．

查看试题解析
26. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根比另一个根大1，那么称这样的方程为“邻根方程”；例如，一元二次方程 $x^{2} + x = 0$ 的两个根是 $x_{1} = 0 ， x_{2} = - 1$ ，则方程 $x^{2} + x = 0$ 是“邻根方程”．

(1)、根据上述定义，判断方程 $2 x^{2} - 2 \sqrt{3} x + 1 = 0$ （填“是”或“不是”）“邻根方程”；

(2)、已知关于x的方程 $x^{2} - (m - 1) x - m = 0 (m$ 是常数 $)$ 是“邻根方程”，求m的值；

(3)、若关于x的方程 $a x^{2} + b x + 1 = 0 (a$ 、b是常数， $a > 0)$ 是“邻根方程”，令 $t = 12 a - b^{2}$ ，试求t的最大值．

查看试题解析
27. 在平面内，O为线段AB的中点，所有到点O的距离等于OA的点组成图形W．取OA的中点C，过点C作CD⊥AB交图形W于点D，D在直线AB的上方，连接AD，BD．

(1)、求∠ABD的度数；

(2)、若点E在线段CA的延长线上，且∠ADE＝∠ABD，求直线DE与图形W的公共点个数．

查看试题解析