江苏省苏州市高新区2021-2022学年九年级上学期第一次月考数学试卷
试卷更新日期:2022-08-09 类型:月考试卷
一、单选题
-
1. 下面四组线段中,成比例的是( )A、a=2,b=3,c=4,d=5 B、a=1,b=2,c=2,d=4 C、a=4,b=6,c=8,d=10 D、a= ,b= ,c=3,d=2. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、143. 线段 , P是AB的黄金分割点,且 , 则BP的长度为A、 B、 C、 D、4. 如图,▱ABCD中,点E是AD的中点,EC交对角线BD于点F,则 ( )
 A、 B、2 C、 D、5. 下列说法中,正确的是( )
A、 B、2 C、 D、5. 下列说法中,正确的是( )
A、等弦所对的弧相等 B、等弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等6. 下列各选项中的两个图形不是位似图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个8. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
7. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个8. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( ) A、1.2m B、1.3m C、1.4m D、1.5m9. 如图,在等腰△ABC中,∠ABC=∠ACB=α,BC=12,点D是边AB上一点,且BD=4,点P是边BC上一动点,作∠DPE=α,射线PE交边AC于点E , 当CE=9时,则满足条件的P点的个数是( )
A、1.2m B、1.3m C、1.4m D、1.5m9. 如图,在等腰△ABC中,∠ABC=∠ACB=α,BC=12,点D是边AB上一点,且BD=4,点P是边BC上一动点,作∠DPE=α,射线PE交边AC于点E , 当CE=9时,则满足条件的P点的个数是( )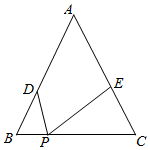 A、1 B、2 C、3 D、以上都有可能10. 如图,正方形 中, 为 中点,连接 , 于点 ,连接 , 交 于点 ,下列结论:① ;② 为 中点;③ ;④ ,其中结论正确的个数有( )
A、1 B、2 C、3 D、以上都有可能10. 如图,正方形 中, 为 中点,连接 , 于点 ,连接 , 交 于点 ,下列结论:① ;② 为 中点;③ ;④ ,其中结论正确的个数有( )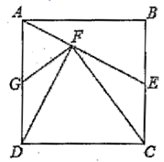 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在比例尺为的旅游地图上,某条道路的长为3cm,则这条道路的实际长度为km.12. 若 , 则.13. 如图,点A、B、C、D在⊙O上, ,则ACBD(填“>”“<”或“=”)
 14. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是15. 如图,在中, , , , 平分 , , 则的长是 .
14. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是15. 如图,在中, , , , 平分 , , 则的长是 . 16. 一块含有 角的直角三角板 按如图所示的方式放置,若顶点A的坐标为 ,直角顶点C的坐标为 ,则点B的坐标为.
16. 一块含有 角的直角三角板 按如图所示的方式放置,若顶点A的坐标为 ,直角顶点C的坐标为 ,则点B的坐标为. 17. 如图:中, , , , 把边长分别为 , , , 的个正方形依次放在中:第一个正方形的顶点分别放在的各边上;第二个正方形的顶点分别放在△的各边上,其他正方形依次放入,则第2022个正方形的边长x2022为 .
17. 如图:中, , , , 把边长分别为 , , , 的个正方形依次放在中:第一个正方形的顶点分别放在的各边上;第二个正方形的顶点分别放在△的各边上,其他正方形依次放入,则第2022个正方形的边长x2022为 . 18. 已知点是反比例函数图象上的动点,轴,轴,分别交反比例函数的图象于点B、C,交坐标轴于D、E,且 , 连接.现有以下四个结论:①;②在点A运动过程中,的面积始终不变;③连接 , 则;④不存在点A,使得.其中正确的结论的序号是 .
18. 已知点是反比例函数图象上的动点,轴,轴,分别交反比例函数的图象于点B、C,交坐标轴于D、E,且 , 连接.现有以下四个结论:①;②在点A运动过程中,的面积始终不变;③连接 , 则;④不存在点A,使得.其中正确的结论的序号是 .
三、解答题
-
19. 解下列一元二次方程:(1)、x2+x=0;(2)、x2﹣4x﹣7=0.20. 已知:如图,A,B,C,D是⊙O上的点,且AB=CD,求证:∠AOC=∠BOD.
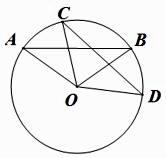 21. 如图,在 中,点D在 边上, .
21. 如图,在 中,点D在 边上, . (1)、求证: ;(2)、若 求 的长.22. 如图,O为原点,B,C两点坐标分别为(3,−1) ,(2,1).
(1)、求证: ;(2)、若 求 的长.22. 如图,O为原点,B,C两点坐标分别为(3,−1) ,(2,1). (1)、以O为位似中心在y轴左侧将ΔOBC放大两倍,并画出图形;(2)、分别写出B,C两点的对应点B′,C′的坐标;(3)、已知M(x,y)为ΔOBC内部一点,写出M的对应点M′的坐标.23. 已知如图,AD是ABC的中线,且 , E为AD上一点, .
(1)、以O为位似中心在y轴左侧将ΔOBC放大两倍,并画出图形;(2)、分别写出B,C两点的对应点B′,C′的坐标;(3)、已知M(x,y)为ΔOBC内部一点,写出M的对应点M′的坐标.23. 已知如图,AD是ABC的中线,且 , E为AD上一点, . (1)、求证:;(2)、若 , , 试求线段AD的长.24. 如图所示,晚上小亮走在大街上,他发现当他站在大街上高度相等的两盏路灯AB和CD之间时,自己右边的影子NE的长为3m,左边的影子ME的长为1.5m,又知小亮的身高EF为1.80m,两盏路灯AC之间的距离为12m,点A、M、E、N、C在同一条直线上,问:路灯的高为多少米?
(1)、求证:;(2)、若 , , 试求线段AD的长.24. 如图所示,晚上小亮走在大街上,他发现当他站在大街上高度相等的两盏路灯AB和CD之间时,自己右边的影子NE的长为3m,左边的影子ME的长为1.5m,又知小亮的身高EF为1.80m,两盏路灯AC之间的距离为12m,点A、M、E、N、C在同一条直线上,问:路灯的高为多少米? 25. 如图,在RtΔABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
25. 如图,在RtΔABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE. (1)、若∠ABC=20°,求∠DEA的度数;(2)、若AC=3,AB=4,求CD的长.26. 如图,矩形 内接于 (矩形各顶点在三角形边上), , 在 上, , 分别在 , 上,且 于点 ,交 于点 .
(1)、若∠ABC=20°,求∠DEA的度数;(2)、若AC=3,AB=4,求CD的长.26. 如图,矩形 内接于 (矩形各顶点在三角形边上), , 在 上, , 分别在 , 上,且 于点 ,交 于点 . (1)、求证: ;(2)、若 , ,设 ,矩形 的面积为 ,求出 与 之间的函数表达式,并写出自变量 的取值范围.27. 已知:如图,等边中,点D、E分别在、边上,且 , 、相交于点O,连接 .
(1)、求证: ;(2)、若 , ,设 ,矩形 的面积为 ,求出 与 之间的函数表达式,并写出自变量 的取值范围.27. 已知:如图,等边中,点D、E分别在、边上,且 , 、相交于点O,连接 . (1)、如图1,当时,的度数为 ;(2)、如图2,当时,
(1)、如图1,当时,的度数为 ;(2)、如图2,当时,①求的值;
②求证: .
28. 矩形ABCD中,AB=6cm,BC=8cm,设运动时间为t(单位:s). (1)、(1)如图1,若动点P从矩形ABCD的顶点A出发,沿A→B→C匀速运动到点C,图2是点P运动时,ΔAPC的面积S(cm2)随时间t(秒)变化的函数图象.
(1)、(1)如图1,若动点P从矩形ABCD的顶点A出发,沿A→B→C匀速运动到点C,图2是点P运动时,ΔAPC的面积S(cm2)随时间t(秒)变化的函数图象.①点P的运动速度是____cm/s,m+n=____;
②若PC=2PB,求t的值;
(2)、如图3,若点P,Q,R分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,当点Q到达点C(即点Q与点C重合)时,三个点随之停止运动;若点P运动速度与(1)中相同,且点P,Q,R的运动速度的比为2:4:3,是否存在t,使ΔPBQ与ΔQCR相似,若存在,求出所有的t的值;若不存在,请说明理由.