江苏省南京市三校2021-2022学年九年级上学期数学第一次联考试卷

试卷更新日期：2022-08-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 若关于 $x$ 的一元二次方程 $x^{2} - 3 x + a = 0$ 的一个根为1，则 $a$ 的值为（）

A、2 B、3 C、－2 D、－1

查看试题解析
2. 有一个圆的半径为5，则该圆的弦长不可能是（）

A、1 B、4 C、10 D、11

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x - 1 = 0$ ，则方程可变形为（）．

A、 ${(x + 3)}^{2} = 10$ B、 ${(x - 3)}^{2} = 10$ C、 ${(x - 3)}^{2} = 8$ D、 ${(x + 3)}^{2} = 8$

查看试题解析
4. 如果长方形的宽增加 $1$ $c m$ ，长减少1 $c m$ ，那么其面积增加 $3$ $c m^{2}$ ．已知原长方形的面积为 $12$ $c m^{2}$ ，则原长方形的长和宽分别为（）

A、 $7$ $c m$ ， $3$ $c m$ B、 $6$ $c m$ ， $2$ $c m$ C、 $4$ $c m$ ， $3$ $c m$ D、 $5$ $c m$ ， $2.4$ $c m$

查看试题解析
5. 已知AB是⊙O的直径，过点A的弦AD平行于半径OC，若∠A＝70°，则∠B等于（）

A、30° B、35° C、40° D、60°

查看试题解析
6. 如图，AB是半⊙O的直径，点C在半⊙O上，AB＝5cm，AC＝4cm.D是 $\overset{⌢}{B C}$ 上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为（）

A、1 B、 $\sqrt{13}$ ﹣2 C、2 $\sqrt{2}$ ﹣1 D、3

查看试题解析

二、填空题

7. 一元二次方程 $x^{2} = 3 x$ 的解为.

查看试题解析
8. 若一个一元二次方程的两个根分别是1、3，请写出一个符合题意的一元二次方程．

查看试题解析
9. 一个扇形的半径长为6，面积为 $8 π$ ，这个扇形的圆心角是度.

查看试题解析
10. 如图，正六边形 $A B C D E F$ 的面积是 $24 \sqrt{3}$ ，则对角线 $A D$ 的长是．

查看试题解析
11. 如果圆锥的底面半径为3cm，母线长为6cm，那么它的侧面积等于 ${cm}^{2}$ .

查看试题解析
12. 对于实数a，b，我们定义一种运算“※”为：a※b＝a²－ab，例如1※3＝1²－1×3．若x※4＝0，则x＝．

查看试题解析
13. 若关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等实数跟，则k的取值范围是．

查看试题解析
14. 如图，甲船从点O出发，自南向北以40海里/时的速度行驶；乙船在点O正东方向120海里的A处，以30海里/时的速度自东向西行驶，经过小时两船的距离为100海里．

查看试题解析
15. 在边长为 $\sqrt{3}$ 的正方形OABC中，D为边BC上一点，且CD＝1，以O为圆心，OD为半径作圆，分别与OA、OC的延长线交于点E、F，则阴影部分的面积为．

查看试题解析
16. 如图，AB是半圆O的直径，点C在半圆O上，AB=5cm，AC=4cm．D是弧BC上的一个动点（含端点B，不含端点C），连接AD，过点C作CE⊥AD于E，连接BE，在点D移动的过程中，BE的取值范围是．

查看试题解析

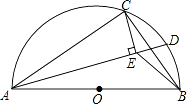
三、解答题

17. 解方程：

(1)、x²﹣5x﹣6＝0；

(2)、4x²﹣8x+1＝0．

查看试题解析
18. 用一根长为 $24 cm$ 的铁丝，围成一个矩形 $A B C D$ ，请用所学的方程或函数知识解答：矩形 $A B C D$ 的面积是否可以为 $38 {cm}^{2}$ ？若能，请求出该矩形的边长；若不能，请说明理由．

查看试题解析
19. 如图， $A B$ 是 $⊙ O$ 的弦， $C$ 为 $A B$ 的中点， $O C$ 的延长线与 $⊙ O$ 交于点 $D$ ，若 $C D = 2$ ， $A B = 12$ ，求 $⊙ O$ 的半径．

查看试题解析
20. 如图，⊙O的直径AB与弦CD相交于E，已知AE＝1cm，BE＝5cm，∠DEB＝30°，求：

(1)、CD的弦心距OF的长；

(2)、弦CD的长．

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点， $D$ 在 $A B$ 上，且 $A D = A C$ ， $C D$ 的延长线与 $⊙ O$ 交于点 $E$ ．

(1)、求证： $∠ C A B = 2 ∠ B C E$ ；

(2)、若 $A B = 4$ ， $C E = 2 \sqrt{2}$ ，求 $∠ B C E$ 的度数

查看试题解析
22. 已知关于x的方程x²﹣2（m+1）x+m²﹣3＝0的两实根为x₁ ， x₂.

(1)、求m的取值范围；

(2)、如果x₁²+x₂²＝x₁x₂+33，求m的值.

查看试题解析
23. 为满足市场需求，新生活超市在端午节前夕购进价格为3元/个的粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个．为了维护消费者利益，物价部门规定，该品牌粽子的售价不能超过进价的200%．

(1)、该品牌粽子每个售价为5元，则每天出售个．

(2)、该品牌粽子定价为多少元时，该超市每天的销售利润为800元．

查看试题解析
24. 如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC＝CD，∠D＝30°，

(1)、请判断CD是否⊙O的切线？并说明理由；

(2)、若⊙O的半径为6，求弧AC的长．（结果保留π）

查看试题解析
25. 某汽车销售公司2017年10月份销售一种新型低能耗汽车20辆，由于该型号汽车经济适用性强，销量快速上升，12月份该公司销售该型号汽车达45辆．

(1)、求11月份和12月份的平均增长率；

(2)、该型号汽车每辆的进价为10万元，且销售a辆汽车，汽车厂队销售公司每辆返利0.03a万元，该公司这种型号汽车的售价为11万元/辆，若使2018年1月份每辆汽车盈利不低于2.6万元，那么该公司1月份至少需要销售该型号汽车多少辆？此时总盈利至少是多少万元？（盈利＝销售利润+返利）

查看试题解析
26. 用54m长的竹栅栏围一个矩形菜园，菜园的一边靠墙的长为am，另三边用竹栅栏围成，且在与墙平行的一边开两扇门，宽度都是1m，设与墙垂直的一边长为xm．

(1)、当a＝41时，矩形菜园面积是320m² ，求x；

(2)、当a足够大时，问矩形菜园的面积能否达到400m²？

(3)、若矩形菜园的面积是320m² ， x的值只能取一个，试写出a的取值范围．

查看试题解析
27. 如图，AB是⊙O的直径，点P在⊙O上，且PA＝PB，点M是⊙O外一点，MB与⊙O相切于点B，连接OM，过点A作AC∥OM交⊙O于点C，连接BC交OM于点D.

(1)、求证：OD＝ $\frac{1}{2}$ AC；

(2)、求证：MC是⊙O的切线；

(3)、若 $O B = \frac{15}{2}$ ，BC＝12，连接PC，求PC的长.

查看试题解析

江苏省南京市三校2021-2022学年九年级 上学期数学第一次联考试卷

一、单选题

二、填空题

三、解答题

江苏省南京市三校2021-2022学年九年级上学期数学第一次联考试卷