(鲁教版)2022-2023学年度第一学期七年级数学第二章 轴对称 单元测试
试卷更新日期:2022-08-09 类型:单元试卷
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
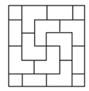 B、
B、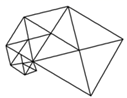 C、
C、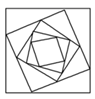 D、
D、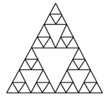 2. 将一张等腰三角形纸片按图①所示的方式对折,再按图②所示的虚线剪去一个小三角形,将余下纸片展开得到的图形是( )
2. 将一张等腰三角形纸片按图①所示的方式对折,再按图②所示的虚线剪去一个小三角形,将余下纸片展开得到的图形是( )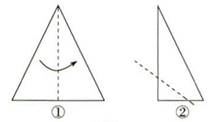 A、
A、 B、
B、 C、
C、 D、
D、 3. 周长38的三角形纸片(如图甲), , 将纸片按图中方式折叠,使点A与点B重合,折痕为(如图乙),若的周长为25 , 则的长为( )
3. 周长38的三角形纸片(如图甲), , 将纸片按图中方式折叠,使点A与点B重合,折痕为(如图乙),若的周长为25 , 则的长为( )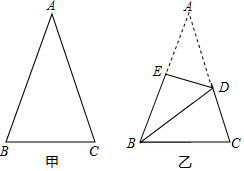 A、10 B、12 C、15 D、134. 如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )
A、10 B、12 C、15 D、134. 如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )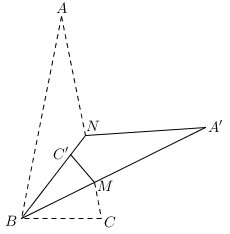 A、87° B、84° C、75° D、72°5. 如图,直线l是线段AB的垂直平分线,点C在直线l外,且与点A在直线l的同侧,点P是直线l上的任意一点,连接AP,BC,CP,则BC与AP+PC的大小关系是( )
A、87° B、84° C、75° D、72°5. 如图,直线l是线段AB的垂直平分线,点C在直线l外,且与点A在直线l的同侧,点P是直线l上的任意一点,连接AP,BC,CP,则BC与AP+PC的大小关系是( )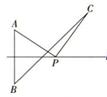 A、BC>AP+PC B、BC<AP+PC C、BC≥AP+PC D、BC≤AP+PC6. 如图,AC=BC , ∠ACB=90°,AE平分∠BAC交BC于点D , BF⊥AE , 交AC的延长线于点F , 且垂足为E , 则下列结论①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF:⑤AD=2BE . 其中正确的结论有( )个
A、BC>AP+PC B、BC<AP+PC C、BC≥AP+PC D、BC≤AP+PC6. 如图,AC=BC , ∠ACB=90°,AE平分∠BAC交BC于点D , BF⊥AE , 交AC的延长线于点F , 且垂足为E , 则下列结论①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF:⑤AD=2BE . 其中正确的结论有( )个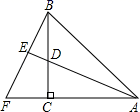 A、5 B、4 C、3 D、27. 如图,AB=AC , 点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为 ACE中CE边上的中线,则∠ADB的度数为( )
A、5 B、4 C、3 D、27. 如图,AB=AC , 点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为 ACE中CE边上的中线,则∠ADB的度数为( )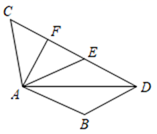 A、24° B、28° C、30° D、38°8. 如图,在 ABC中,AC=5,AB=7,AD平分∠BAC , DE⊥AC , DE=3,则 ABC的面积为( )
A、24° B、28° C、30° D、38°8. 如图,在 ABC中,AC=5,AB=7,AD平分∠BAC , DE⊥AC , DE=3,则 ABC的面积为( )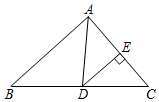 A、72 B、36 C、18 D、99.
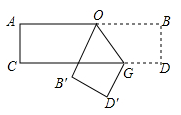
A、72 B、36 C、18 D、99.用边长为1的正方形纸板制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),则图②中∠ABC+∠GEB=( )
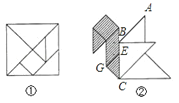 A、360° B、270° C、225° D、180°10. 如图,将一块边长为8的正方形张片制作成一幅七巧板,并拼成右边的图案“一座桥”,则桥的中间阴影部分的面积为( )
A、360° B、270° C、225° D、180°10. 如图,将一块边长为8的正方形张片制作成一幅七巧板,并拼成右边的图案“一座桥”,则桥的中间阴影部分的面积为( )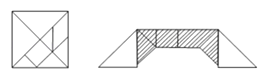 A、16 B、24 C、32 D、48
A、16 B、24 C、32 D、48二、填空题
-
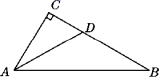
11. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=3,AB=10,则△ABD的面积为 .
 12. 已知等腰三角形的一边长为5,另一边长为10,则这个等腰三角形的周长为 .13. 七巧板是一种古老的中国传统智力玩具,顾名思义,是由七块板组成的.清陆以潘《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.玩家也可以把它拼成各种人物、形象、动物、桥、房、塔等等.小明用一块边长为 的正方形的厚纸板,做了一套七巧板(如图甲).小聪用小明做的七巧板拼成一座桥(如图乙),这座桥的阴影部分的面积是 .
12. 已知等腰三角形的一边长为5,另一边长为10,则这个等腰三角形的周长为 .13. 七巧板是一种古老的中国传统智力玩具,顾名思义,是由七块板组成的.清陆以潘《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.玩家也可以把它拼成各种人物、形象、动物、桥、房、塔等等.小明用一块边长为 的正方形的厚纸板,做了一套七巧板(如图甲).小聪用小明做的七巧板拼成一座桥(如图乙),这座桥的阴影部分的面积是 .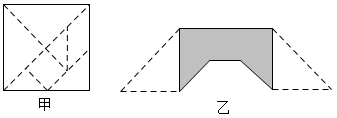 14. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.
14. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.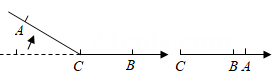 15. 如图,长方形ABCD点E,F分别在边AB,CD上,连接EF将∠BEF对折,点B落在直线EF上的点处,得折痕EM;将∠AEF对折,点A落在直线EF上的点处,得折痕EN,点G在CD上, , 则∠BEM为度.
15. 如图,长方形ABCD点E,F分别在边AB,CD上,连接EF将∠BEF对折,点B落在直线EF上的点处,得折痕EM;将∠AEF对折,点A落在直线EF上的点处,得折痕EN,点G在CD上, , 则∠BEM为度.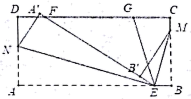
三、解答题
-
16. 如图,把一张长方形的纸按图那样折叠后, 两点落在 点处,若 ,求 的度数.
 17. 按下面的方法折纸,然后回答问题:
17. 按下面的方法折纸,然后回答问题: (1)、∠1与∠AEC有何关系?(2)、∠1,∠3有何关系?(3)、∠2是多少度的角?请说明理由.18.
(1)、∠1与∠AEC有何关系?(2)、∠1,∠3有何关系?(3)、∠2是多少度的角?请说明理由.18.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设△AED的度数为x , ∠ADE的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
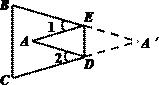
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.19. 如图,在△ABC中,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,D是BC的中点,证明:∠B=∠C.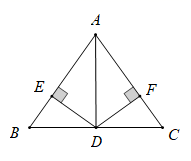 20. 如图,若 和 都是等边三角形,求 的度数.
20. 如图,若 和 都是等边三角形,求 的度数.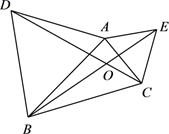 21. 已知: , , 平分 .求: 的度数.22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
21. 已知: , , 平分 .求: 的度数.22. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).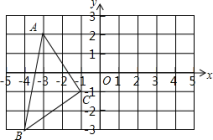
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
23. 如图(1),把△ABC沿直线BC平行移动线段BC的长度,可以变到△DEC的位置;如图(2),以BC为轴,把△ABC翻折180°,可以变到△DBC的位置;
如图(3),以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状、大小的图形变换叫做全等变换.以上三种变换分别为平行移动、翻折、旋转变换.
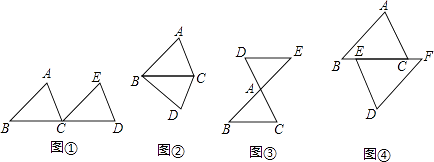
问题:如图(4),△ABC≌△DFE,D和A、B和F、C和E是对应顶点,问通过怎样的全等变换可以使它们重合.
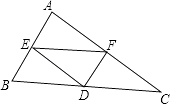
24. 如图,EF∥BC,ED∥AC,FD∥AB,请你写出△AEF由图中哪些三角形可以通过一次平移或旋转而得到.