（鲁教版）2022-2023学年度第一学期七年级数学2.3 简单的轴对称图形同步测试

试卷更新日期：2022-08-09 类型：同步测试

进入出卷网下载

一、单选题

1. 如图， $△$ ABC中，∠A＝90°，AB＝AC，BD平分∠ABC，DE⊥BC，如果BC＝8cm，则 $△$ DEC的周长是（）

A、6cm B、8cm C、9cm D、10cm

查看试题解析
2. 如图，在△ABC中， AB的垂直平分线交BC于D，AC的中垂线交BC于E，∠BAC=124°，则∠DAE的度数为（）

A、68° B、62° C、66° D、56°

查看试题解析
3. 如图，BM是△ABC的角平分线，D是BC边上的一点，连接AD，使AD=DC，且∠BAD=120°，则∠AMB=（）

A、30° B、25° C、22.5° D、20°

查看试题解析
4. 如图，在 $Δ A B C$ 中， $∠ A C B = 90 ° ， B E$ 平分 $∠ A B C ， E D ⊥ A B$ 于 $D$ ．如果 $∠ A = 30 °$ ， $A E = 8 c m$ ，那么 $C E =$ （）

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $5 c m$

查看试题解析
5. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ，以点A为圆心，小于 $A C$ 的长为半径作弧，分别交 $A B$ ， $A C$ 于 $M ， N$ 两点；再分别以点 $M ， N$ 为圆心，大于 $\frac{1}{2} M N$ 长为半径作弧，两弧交于点P，作射线 $A P$ 交 $B C$ 于点D.若 $Δ A B C$ 的面积为9，则 $Δ A C D$ 的面积为（）

A、3 B、 $\frac{9}{2}$ C、6 D、 $\frac{15}{2}$

查看试题解析
6. 如图， $△ A B C$ 中， $∠ A B C$ 与 $∠ A C B$ 的平分线交于点F，过点F作 $D E / / B C$ 交 $A B$ 于点D，交 $A C$ 于点E，那么下列结论，其中正确的有（）
① $△ B D F$ 是等腰三角形；② $D E = B D + C E$ ；③若 $∠ A = 50 °$ ，则 $∠ B F C = 115 °$ ；④ $D F = E F$ ．

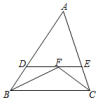A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，若AN=1，则BC的长为（　　）

A、4 B、6 C、 $4 \sqrt{3}$ D、8

查看试题解析
8. 已知等腰三角形一腰上的高线与另一腰的夹角为 $40 °$ ，那么这个等腰三角形的顶角等于（）．

A、 $50 °$ 或 $130 °$ B、 $130 °$ C、 $80 °$ D、 $50 °$ 或 $80 °$

查看试题解析
9. 如图，在 $△ A B C$ 中， $D E$ 是 $A C$ 的垂直平分线， $A E = 3 cm$ ， $△ A B D$ 的周长为 $13cm$ ，则 $△ A B C$ 的周长是（）．

A、 $13cm$ B、 $16cm$ C、 $19cm$ D、 $22cm$

查看试题解析
10. 如图，已知 $∠ A O B$ ，按下面步骤作图：

（1）在射线 $O A$ 上任意取一点 $C$ ，以点 $O$ 为圆心， $O C$ 长为半径作弧 $M N$ ，交射线 $O B$ 于点 $D$ ，连接 $C D$ ；（2）分别以点 $C$ ， $D$ 为圆心， $C D$ 长为半径作弧，两弧在 $∠ A O B$ 内部交于点 $E$ ，连接 $C E$ ， $D E$ ；（3）作射线 $O E$ 交 $C D$ 于点 $F$ ．

根据以上所作图形，有如下结论，其中错误的是（）．

A、 $C E ∥ O B$ B、 $∠ A O E = ∠ B O E$ C、 $C E = 2 C F$ D、 $C D ⊥ O E$

查看试题解析

二、填空题

11. 如图，在Rt△ABC中，∠A＝90°，∠ABC的平分线BD交AC于点D，AD＝2，BC＝6，则△BDC的面积是．

查看试题解析
12. 如图，△ABC中，DE垂直平分边AC，若BC＝8，AB＝10，则△EBC的周长为．

查看试题解析
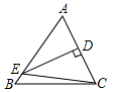13. 在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为．

查看试题解析
14. 如图，在三角形纸片ABC中，∠C＝90°，∠A＝30°，AC＝6，折叠该纸片，使点C落在AB边上的D点处，折痕BE与AC交于点E，则折痕BE的长为．

查看试题解析
15. 如图，∠MON＝30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，从左起第1个等边三角形的边长记为a₁ ，第2个等边三角形的边长记为a₂ ，以此类推.若OA₁＝1，则a₂₀₂₀＝.

查看试题解析

三、解答题

16. 在 $△ A B C$ 中，AB=AC， $∠ B A C = 120 °$ ， AB的垂直平分线交BC于M，交AB与E，AC的垂直平分线交BC 于N ，交AC于F，求证：BM=MN=NC．

查看试题解析
17. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 中点， $D E ⊥ A C$ ，垂足为 $E$ ．若 $∠ B A C = 50 °$ ，求 $∠ A D E$ 的度数．

查看试题解析
18. 如图，在 $△$ ABC中，∠B＝90°，∠A＝30°．作边AC的垂直平分线交AB于点D ，交AC于点E ，连接CD ，已知BD=4，求∠BCD的度数及AD的长．

查看试题解析
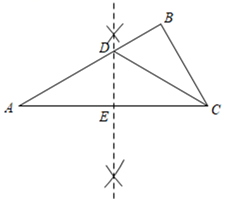19. 尺规作图：如图，某地有两个工厂M、N和两条相交叉的公路a，b现计划修建一座物资仓库，希望仓库到两个工厂的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．(保留作图痕迹)．

查看试题解析
20. 如图，在△ABC中，D、E是边BC上两点，且∠ADC=∠AEB，∠B=∠C，求证：△BAD≌△CAE．

查看试题解析
21. 上午8时，一条船从港口A出发，以15海里/时的速度向正北方向航行，10时到达海岛B处，从A，B两处望灯塔C，分别测得∠NAC=15°，∠NBC=30°．若该船从海岛B继续向正北航行，求船与灯塔C的最短距离．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于D ， E是 $A B$ 上的一点， $E F / / A D$ 交 $C A$ 的延长线于F ．求证： $A F = A E$ ．

查看试题解析
23. 如图，在△ABC中，AB=AC，∠A=120°，BC=6，AB的垂直平分线交恩BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F．求证：BM= MN=NC．

查看试题解析
24. 如图所示，AB∥CD，EF= EH，EH平分∠AEG，且∠EHF=15° ，求∠CFH的度数．

查看试题解析

（鲁教版）2022-2023学年度第一学期七年级数学2.3 简单的轴对称图形 同步测试

一、单选题

二、填空题

三、解答题

（鲁教版）2022-2023学年度第一学期七年级数学2.3 简单的轴对称图形同步测试