(鲁教版)2022-2023学年度第一学期七年级数学2.2 探索轴对称的性质 同步测试
试卷更新日期:2022-08-09 类型:同步测试
一、单选题
-
1. 已知长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角有( )
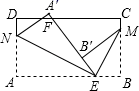 A、2个 B、3个 C、4个 D、5个2. 如图是一纸条的示意图,第1次对折,使A,B两点重合后再打开,折痕为l1;第2次对折,使A,C两点重合后再打开,折痕为l2;第3次对折,使B,D两点重合后再打开,折痕为l3.已知CE=2cm,则纸条原长为( )cm
A、2个 B、3个 C、4个 D、5个2. 如图是一纸条的示意图,第1次对折,使A,B两点重合后再打开,折痕为l1;第2次对折,使A,C两点重合后再打开,折痕为l2;第3次对折,使B,D两点重合后再打开,折痕为l3.已知CE=2cm,则纸条原长为( )cm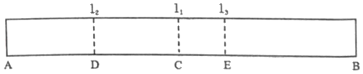 A、18 B、16 C、14 D、123. 如图,将长方形纸片的一角作折叠,使顶点A落在 处,EF为折痕,若 恰好平分∠FEB,则∠FEB的度数为( )
A、18 B、16 C、14 D、123. 如图,将长方形纸片的一角作折叠,使顶点A落在 处,EF为折痕,若 恰好平分∠FEB,则∠FEB的度数为( )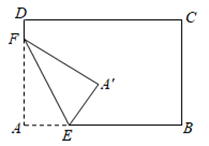 A、60° B、120° C、130° D、100°4. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B' 处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A' 处,得折痕EN.则∠NEM的度数为( )
A、60° B、120° C、130° D、100°4. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B' 处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A' 处,得折痕EN.则∠NEM的度数为( )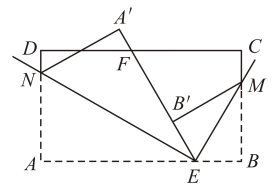 A、105o B、 C、 D、不能确定5. 如图把一张长方形的纸按如图那样折叠后,两点分别落在了点处,若= , 则的度数为( )
A、105o B、 C、 D、不能确定5. 如图把一张长方形的纸按如图那样折叠后,两点分别落在了点处,若= , 则的度数为( )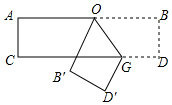 A、 B、 C、 D、6. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,则∠EDF的度数是( )
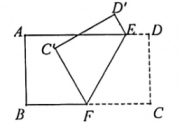
A、 B、 C、 D、6. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,则∠EDF的度数是( )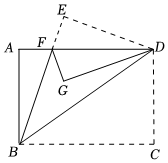 A、18° B、30° C、36° D、20°7. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )
A、18° B、30° C、36° D、20°7. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )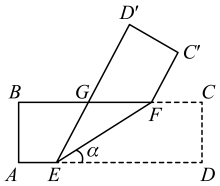 A、2α B、90°+α C、180°﹣α D、180°﹣2α8. 如图,如果直线是△ABC的对称轴,其中∠C=66° ,那么∠BAC的度数等于( )
A、2α B、90°+α C、180°﹣α D、180°﹣2α8. 如图,如果直线是△ABC的对称轴,其中∠C=66° ,那么∠BAC的度数等于( )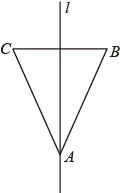 A、66° B、48° C、58° D、24°9. 如图,直线是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,由水泵站直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
A、66° B、48° C、58° D、24°9. 如图,直线是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,由水泵站直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( ) A、
A、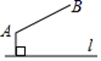 B、
B、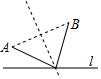 C、
C、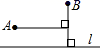 D、
D、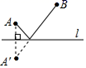 10. 如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF 比 ∠EBF大15°,则∠EBC的度数是( )
10. 如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF 比 ∠EBF大15°,则∠EBC的度数是( ) A、15度 B、20度 C、25度 D、30度
A、15度 B、20度 C、25度 D、30度二、填空题
-
11. 将一张长方形的纸按照如图所示折叠后,点C、D两点分别落在点C'、D'处,若EA平分∠D'EF,则∠DEF= 。
 12. 如图,将ABC沿着DE对折,点A落到处,若 , 则∠A=度.
12. 如图,将ABC沿着DE对折,点A落到处,若 , 则∠A=度.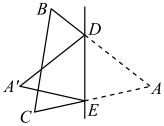 13. 把一个长方形纸片按照如图所示折叠,B的对应点B',C的对应点C'.若∠GOB'=65°,则∠AOB'= .
13. 把一个长方形纸片按照如图所示折叠,B的对应点B',C的对应点C'.若∠GOB'=65°,则∠AOB'= .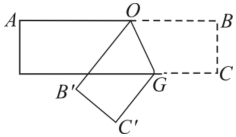 14. 如图,将三角形ABC纸片沿MN折叠,使点A落在点Aʹ处,若∠AʹMB=50°,则∠AMN=度.
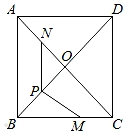
14. 如图,将三角形ABC纸片沿MN折叠,使点A落在点Aʹ处,若∠AʹMB=50°,则∠AMN=度.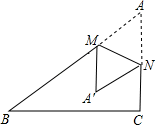 15. 如图,∠AOB内一点P,P1、P2分别是点P关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是 .
15. 如图,∠AOB内一点P,P1、P2分别是点P关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是 .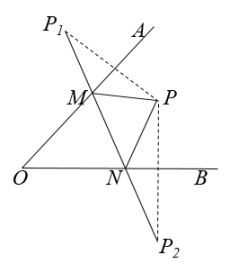
三、解答题
-
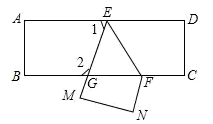
16. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求∠1和∠2的度数.
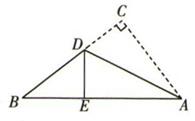
 17. 如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.
17. 如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.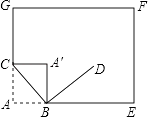 18.
18.如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.
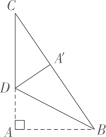
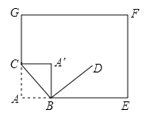 19. 如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为 , 当AC时,求∠BCD的度数.
19. 如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为 , 当AC时,求∠BCD的度数.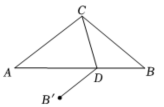 20. 如图,在矩形ABCD中,E是AB的中点,F是为射线AD上的一个动点,将△AEF沿EF折叠得到△HEF,连接AC,分别交EF和直线EH于点N,M,已知∠BAC= , ,若△EMN与△AEF相似,则AF的长为多少?
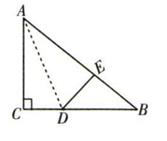
20. 如图,在矩形ABCD中,E是AB的中点,F是为射线AD上的一个动点,将△AEF沿EF折叠得到△HEF,连接AC,分别交EF和直线EH于点N,M,已知∠BAC= , ,若△EMN与△AEF相似,则AF的长为多少?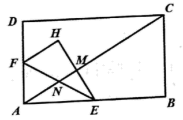 21. 如图,有一直角三角形纸片,两直角边AB=6cm,AC=8cm,现将直角边AB沿直线BD进行对折,使点A刚好落在斜边BC上,且与A'B重合,求BD的长,
21. 如图,有一直角三角形纸片,两直角边AB=6cm,AC=8cm,现将直角边AB沿直线BD进行对折,使点A刚好落在斜边BC上,且与A'B重合,求BD的长,