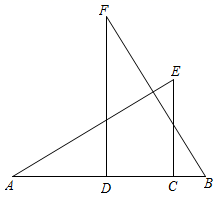(鲁教版)2022-2023学年度第一学期七年级数学第一章 三角形 单元测试
试卷更新日期:2022-08-09 类型:单元试卷
一、单选题
-
1. 已知三角形的两边长分别是4cm和10cm,则下列长度的线段中能作为第三边的是( )A、4cm B、6cm C、8cm D、14cm2. 如图所示,△ABC的边AC上的高是( )
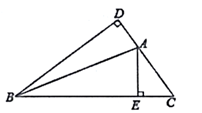 A、线段AE B、线段BA C、线段BD D、线段DA3. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )
A、线段AE B、线段BA C、线段BD D、线段DA3. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )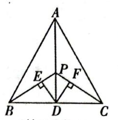 A、1个 B、2个 C、3个 D、4个4. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.连接 , 设正方形的面积为 , 正方形的面积为 , 四边形的面积为.若 , 则下面结论一定正确的是( )
A、1个 B、2个 C、3个 D、4个4. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.连接 , 设正方形的面积为 , 正方形的面积为 , 四边形的面积为.若 , 则下面结论一定正确的是( )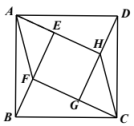 A、 B、 C、 D、5. 如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )
A、 B、 C、 D、5. 如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )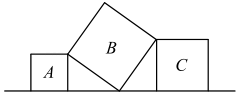 A、26 B、49 C、52 D、646. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )
A、26 B、49 C、52 D、646. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )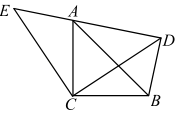 A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形7. 在△ABC中,D是AC上一点,利用尺规在AB上作出一点E,使得 , 则符合要求的作图痕迹是( )A、
A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形7. 在△ABC中,D是AC上一点,利用尺规在AB上作出一点E,使得 , 则符合要求的作图痕迹是( )A、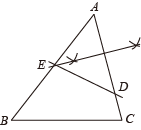 B、
B、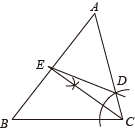 C、
C、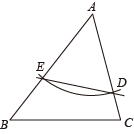 D、
D、 8. 如图,用直尺和圆规作ΔABC和ΔDBC,则ΔABC≌ΔDBC,理由是( )
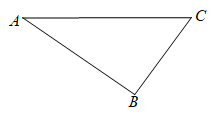
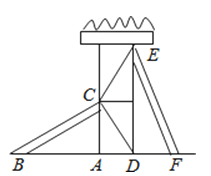
8. 如图,用直尺和圆规作ΔABC和ΔDBC,则ΔABC≌ΔDBC,理由是( )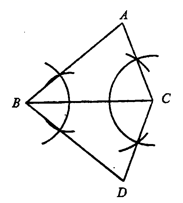 A、SAS B、ASA C、AAS D、SSS9. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是( )
A、SAS B、ASA C、AAS D、SSS9. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明的依据的是( ) A、或 B、或 C、或 D、或10. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A、或 B、或 C、或 D、或10. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )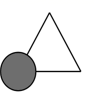 A、AAS B、ASA C、SAS D、SSS
A、AAS B、ASA C、SAS D、SSS二、填空题
-
11. 如图,已知直线l1∥l2 , ∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1=.
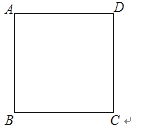
 12. 如图,在矩形中,是的中点,将沿折叠后得到 , 延长交于点点,若 , , 则的长为 .
12. 如图,在矩形中,是的中点,将沿折叠后得到 , 延长交于点点,若 , , 则的长为 .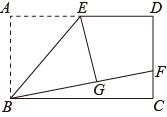 13. 有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为m.
13. 有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为m.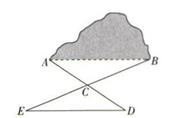 14. 如图,线段 ,用尺规作图法按如下步骤作图.
14. 如图,线段 ,用尺规作图法按如下步骤作图.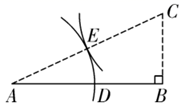
( 1 )过点B作 的垂线,并在垂线上取 ;
( 2 )连接 ,以点C为圆心, 为半径画弧,交 于点E;
( 3 )以点A为圆心, 为半径画弧,交 于点D.即点D为线段 的黄金分割点.
则线段 的长度约为
(结果保留两位小数,参考数据: )
15.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片即可

三、解答题
-
16. 在△ABC.∠A=35°,∠B=69°, CD⊥AB于点D,CE平分∠ACB, DP⊥CE于点P,求∠CDP的度数.
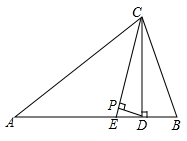 17. 如图,在△ABC中,AD、AE分别是高线与角平分线,∠B=33°,∠C=67°,求∠EAD的度数.
17. 如图,在△ABC中,AD、AE分别是高线与角平分线,∠B=33°,∠C=67°,求∠EAD的度数.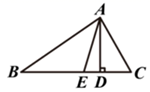 18. 如图,点A、B,C、D在同一条直线上, ,已知 , ,求AD的长.
18. 如图,点A、B,C、D在同一条直线上, ,已知 , ,求AD的长.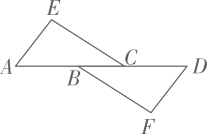 19. 如图,BD平分 ABC的外角∠ABP,DA=DC,DE⊥BP于点E,若AB=5,BC=3,求BE的长.
19. 如图,BD平分 ABC的外角∠ABP,DA=DC,DE⊥BP于点E,若AB=5,BC=3,求BE的长. 20. 如图所示,点E,C,D,A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.试说明:△ABC≌△DEF.
20. 如图所示,点E,C,D,A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.试说明:△ABC≌△DEF. 21. 如图,C,D是线段 上两点, 于点D, 于点C.连接 , .若 , .求证: .
21. 如图,C,D是线段 上两点, 于点D, 于点C.连接 , .若 , .求证: .