(鲁教版)2022-2023学年度第一学期七年级数学1.3 探索三角形全等的条件 同步测试
试卷更新日期:2022-08-09 类型:同步测试
一、单选题
-
1. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形如图所示 , 这样做的数学依据是( )
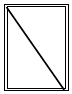 A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短2. 已知:如图,D、E分别在AB、AC上,若AB=AC,AD=AE,∠A=60°,∠B=25°,则∠BDC的度数是( )
A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短2. 已知:如图,D、E分别在AB、AC上,若AB=AC,AD=AE,∠A=60°,∠B=25°,则∠BDC的度数是( )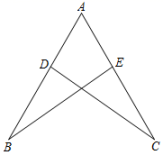 A、95° B、90° C、85° D、80°3. 如图所示, , , , 结论:①;②;③;④ , 其中正确的是有( )
A、95° B、90° C、85° D、80°3. 如图所示, , , , 结论:①;②;③;④ , 其中正确的是有( )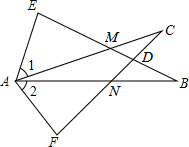 A、1个 B、2个 C、3个 D、4个4. 如图,已知为的中点,若 , 则( )
A、1个 B、2个 C、3个 D、4个4. 如图,已知为的中点,若 , 则( )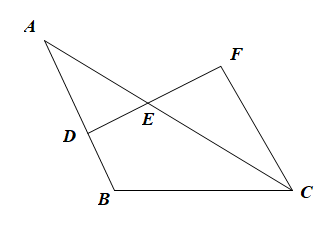 A、5 B、6 C、7 D、5. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
A、5 B、6 C、7 D、5. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )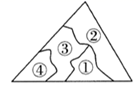 A、第①块 B、第②块 C、第③块 D、第④块6. 如图, 中, , 是 边上的中线,若 ,则 等于( )
A、第①块 B、第②块 C、第③块 D、第④块6. 如图, 中, , 是 边上的中线,若 ,则 等于( )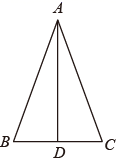 A、 B、 C、 D、7. 如图,点B,C在线段AD上,AB=CD,AE∥BF,添加一个条件仍不能判定△AEC≌△BFD的是( )
A、 B、 C、 D、7. 如图,点B,C在线段AD上,AB=CD,AE∥BF,添加一个条件仍不能判定△AEC≌△BFD的是( )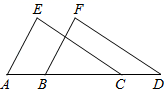 A、AE=BF B、CE=DF C、∠ACE=∠BDF D、∠E=∠F8. 如图, 、 、 、 四点在同一直线上,在 和 中, , ,添加下列条件,仍不能证明 的是( )
A、AE=BF B、CE=DF C、∠ACE=∠BDF D、∠E=∠F8. 如图, 、 、 、 四点在同一直线上,在 和 中, , ,添加下列条件,仍不能证明 的是( )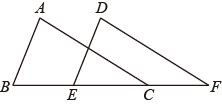 A、 B、 C、 D、9. 如图所示,AB=AD , 添加下列哪个条件仍无法判定△ABC≌△ADE( )
A、 B、 C、 D、9. 如图所示,AB=AD , 添加下列哪个条件仍无法判定△ABC≌△ADE( ) A、∠C=∠E B、BE=DC C、∠CBE=∠EDC D、BC=DE10. 在 和 中,① ,② ,③ ,④ ,⑤ ,⑥ ,则下列( )组条件不能保证 .A、具备①②③ B、具备②④⑤ C、具备①②④ D、具备②③⑥
A、∠C=∠E B、BE=DC C、∠CBE=∠EDC D、BC=DE10. 在 和 中,① ,② ,③ ,④ ,⑤ ,⑥ ,则下列( )组条件不能保证 .A、具备①②③ B、具备②④⑤ C、具备①②④ D、具备②③⑥二、填空题
-
11. 已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是.
 12. 如图, , 要使 , 依据 , 应添加的一个条件是 .
12. 如图, , 要使 , 依据 , 应添加的一个条件是 .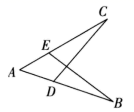 13. 如图, , , , , ,则 .
13. 如图, , , , , ,则 .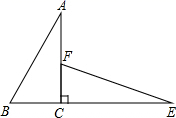 14. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是
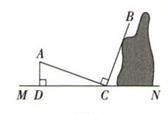
14. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 15. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是cm.
15. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是cm.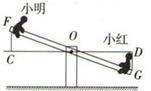
三、解答题
-
16. 如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.
 17. 如图,已知AB=AC,BD=CE,证明△ABE≌△ACD.
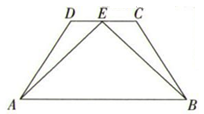
17. 如图,已知AB=AC,BD=CE,证明△ABE≌△ACD.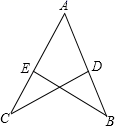 18. 如图,树 与树 之间相距 ,小华从点B沿 走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,且两条视线的夹角正好为 , .已知大树 的高为 ,小华行走的速度为 ,求小华从点B行走到点E的时间.
18. 如图,树 与树 之间相距 ,小华从点B沿 走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,且两条视线的夹角正好为 , .已知大树 的高为 ,小华行走的速度为 ,求小华从点B行走到点E的时间. 19. 如图,已知在等边三角形ABC中,D、E分别是AB、AC上的点,且AD=CE . 求证:CD=BE .
19. 如图,已知在等边三角形ABC中,D、E分别是AB、AC上的点,且AD=CE . 求证:CD=BE .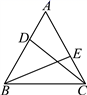 20. 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
20. 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.求证:△BED≌△CFD.
 21. 已知:如图,C是AB的中点,AE=BD,∠A=∠B.
21. 已知:如图,C是AB的中点,AE=BD,∠A=∠B.求证:∠ACE=∠BCD.