(鲁教版)2022-2023学年度第一学期七年级数学1.2 图形的全等 同步测试
试卷更新日期:2022-08-09 类型:同步测试
一、单选题
-
1. 如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
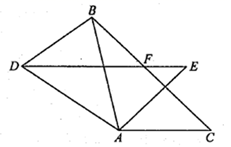
 A、6cm B、5cm C、7cm D、无法确定2. 如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).
A、6cm B、5cm C、7cm D、无法确定2. 如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).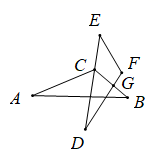 A、 B、 C、 D、3. 如图,若 ,则 等于( )
A、 B、 C、 D、3. 如图,若 ,则 等于( ) A、 B、 C、 D、4. 如图,△ACB≌△A'CB',∠A'CB=30°,∠ACB'=110°,则∠ACA'的度数是( )
A、 B、 C、 D、4. 如图,△ACB≌△A'CB',∠A'CB=30°,∠ACB'=110°,则∠ACA'的度数是( )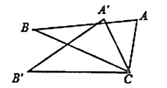 A、20° B、30° C、35° D、40°5. 如图, ,点A和点B , 点C和点D是对应点.如果 , ,那么 度数是( )
A、20° B、30° C、35° D、40°5. 如图, ,点A和点B , 点C和点D是对应点.如果 , ,那么 度数是( )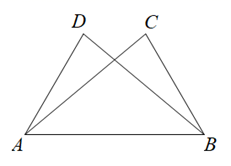 A、80° B、70° C、60° D、50°6. 如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=56°,则∠CAF的度数为( )
A、80° B、70° C、60° D、50°6. 如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=56°,则∠CAF的度数为( ) A、36° B、24° C、56° D、34°7. 下列说法中,正确的是( )A、全等图形是形状相同的两个图形 B、全等三角形是指面积相同的两个三角形 C、等边三角形都是全等三角形 D、全等图形的周长、面积都相等8. 下列选项中的图形与给出的图形全等的是( )
A、36° B、24° C、56° D、34°7. 下列说法中,正确的是( )A、全等图形是形状相同的两个图形 B、全等三角形是指面积相同的两个三角形 C、等边三角形都是全等三角形 D、全等图形的周长、面积都相等8. 下列选项中的图形与给出的图形全等的是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 2002年北京国际数学家大会的会徽是一个“弦图”(如图①),它是由4个全等的直角三角形(不等腰)拼接而成的.如图②,在线段AE和CG上分别取点P和点Q,使AP=CQ,连接DP,BP,DQ,BQ,则构成了一个“压扁”的弦图.问题:线段AE,CG中,是否存在不同于端点的点P,Q,使得“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积依然满足S1=S2=S3=S4?( )
9. 2002年北京国际数学家大会的会徽是一个“弦图”(如图①),它是由4个全等的直角三角形(不等腰)拼接而成的.如图②,在线段AE和CG上分别取点P和点Q,使AP=CQ,连接DP,BP,DQ,BQ,则构成了一个“压扁”的弦图.问题:线段AE,CG中,是否存在不同于端点的点P,Q,使得“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积依然满足S1=S2=S3=S4?( )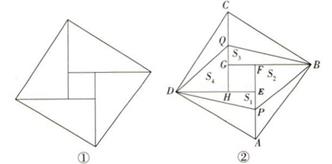 A、存在且唯一 B、存在多个 C、不存在 D、无法确定10. 如图,在四边形 中, .不能判定 的条件是( )
A、存在且唯一 B、存在多个 C、不存在 D、无法确定10. 如图,在四边形 中, .不能判定 的条件是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,△ABC≌△DFE , 点B、E、C、F在同一直线上,BE=2cm , BF=11cm , 则EC的长度是 .
 12. 如图,若 , ,则 .
12. 如图,若 , ,则 . 13. 如图, ,CE=6,FC=2,则BE= .
13. 如图, ,CE=6,FC=2,则BE= .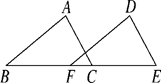 14. 如图,△ABC≌△ADE,且点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 .
14. 如图,△ABC≌△ADE,且点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 .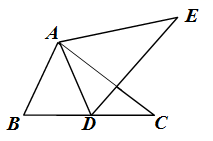 15. 若 , , ,点 的对应点是 , ,那么 的度数是.
15. 若 , , ,点 的对应点是 , ,那么 的度数是.三、解答题
-
16. 在讲完全等三角形后,教数学的王老师布置了一道数学题:如图所示,已知 ,其中 , ,则 与 有何位置关系?请说明理由.
 17. 数学之美,不仅是几何图形经过排列组合后呈现的炫美图案,还包括严谨推理引发的思维律动.已超过400种勾股定理的证明方法呈现的数学之美让我们陶醉,其中一种方法是:将两个全等的和如图所示摆放,使点 , , 在同一条直线上,中,即可借助图中几何图形的面积关系来证明 . 请写出证明过程.
17. 数学之美,不仅是几何图形经过排列组合后呈现的炫美图案,还包括严谨推理引发的思维律动.已超过400种勾股定理的证明方法呈现的数学之美让我们陶醉,其中一种方法是:将两个全等的和如图所示摆放,使点 , , 在同一条直线上,中,即可借助图中几何图形的面积关系来证明 . 请写出证明过程.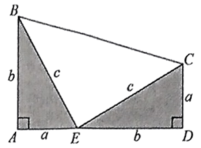 18. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:四边形ABED是平行四边形.
18. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:四边形ABED是平行四边形.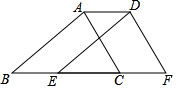 19. 已知:如图,在中,点O是的中点,连接并延长,交的延长线于点E,求证: .
19. 已知:如图,在中,点O是的中点,连接并延长,交的延长线于点E,求证: . 20. 如图,线段AD上有两点E,B,且AE=DB,分别以AB,DE为直角边在线段AD同侧作Rt△ABC和Rt△DEF,∠A=∠D=90°,BC=EF.求证:∠AEG=∠DBG.
20. 如图,线段AD上有两点E,B,且AE=DB,分别以AB,DE为直角边在线段AD同侧作Rt△ABC和Rt△DEF,∠A=∠D=90°,BC=EF.求证:∠AEG=∠DBG. 21. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: .
21. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: .