江苏省常州市2021-2022学年高二下学期数学期末考试试卷

试卷更新日期：2022-08-08 类型：期末考试

进入出卷网下载

一、单选题

1. 甲、乙、丙3名数学竞赛获奖同学邀请2名指导教师站在一排合影留念，若2名教师不相邻，且教师不站在两端，则不同的站法种数是（）

A、6 B、12 C、24 D、48

查看试题解析
2. 疫情期间，学校进行网上授课，某中学参加网课的100名同学每天的学习时间（小时）服从正态分布 $N (9 ， 1^{2})$ ，则这些同学中每天学习时间超过10小时的人数估计为（）
附：随机变量ξ服从正态分布N（μ，σ²），则P（μ－σ＜ξ＜μ＋σ）＝0.6826，P（μ－2σ＜ξ＜μ＋2σ）＝0.9544，P（μ－3σ＜ξ＜μ＋3σ）＝0.9974．

A、14 B、16 C、30 D、32

查看试题解析
3. 现有4名医生分别到A，B，C三所医院支援抗疫，每名医生有且只能去一所医院且每所医院至少去一名医生，则甲、乙两医生恰好到同一医院支援的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
4. 已知二面角 $α - l - β$ ，其中平面的一个法向量 $\vec{m} = (1 ， 0 ， - 1)$ ，平面 $β$ 的一个法向量 $\vec{n} = (0 ， - 1 ， 1)$ ，则二面角 $α - l - β$ 的大小可能为（）

A、60° B、120° C、60°或120° D、30°

查看试题解析
5. 我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果，功不可没，“三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液；“三方”分别为清肺排毒汤、化败毒方、宣肺败毒方.若某医生从“三药三方”中随机选出两种，事件 $A$ 表示选出的两种中有一药，事件 $B$ 表示选出的两种中有一方，则 $P (B | A) =$ （）

A、 $\frac{1}{5}$ B、 $\frac{3}{10}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析
6. $(x + \frac{a}{x}) {(2 x - \frac{1}{x})}^{5}$ 的展开式中各项系数的和为2，则该展开式中常数项为（）

A、-40 B、-20 C、20 D、40

查看试题解析
7. 如图，在棱长为2的正方体ABCDA₁B₁C₁D₁中，E为BC的中点，点P在线段D₁E上，点P到直线CC₁的距离的最小值为（　　）

A、 $\frac{2}{5} \sqrt{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{10}$ D、 $\frac{3}{10} \sqrt{5}$

查看试题解析
8. 数列{an}满足a₁＝1， $a_{n + 1} = \frac{a_{n}}{a_{n} + 2} (n \in N^{*})$ ，若 $b_{n + 1} = (n - 2 λ) (\frac{1}{a_{n}} + 1) (n \in N^{*})$ ， b₁＝－λ，且数列{bn}满足bn_＋₁＞bn（n∈N*），则实数λ的取值范围是（）

A、 $λ > \frac{2}{3}$ B、 $λ > \frac{3}{2}$ C、 $λ < \frac{2}{3}$ D、 $λ < \frac{3}{2}$

查看试题解析

二、多选题

9. 北京冬奥会成功举办后，大众对冰雪运动关注度不断上升，为研究市民对冰雪运动的喜好是否和性别有关，某校学生社团对市民进行了一次抽样调查，得到列联表如下：
冰雪运动的喜好
性别
合计
男性
女性
喜欢
140
m
140＋m
不喜欢
n
80
80＋n
合计
140＋n
80＋m
220＋m＋n
若男性喜欢冰雪运动的人数占男性人数 $\frac{7}{10}$ ，女性喜欢冰雪运动的人数占女性人数 $\frac{3}{5}$ ，则（）

A、列联表中n的值为60，m的值为120 B、随机对一位路人进行调查，有95%的可能性对方喜欢冰雪运动 C、有95%的把握认为市民对冰雪运动的喜好和性别有关 D、没有99%的把握认为市民对冰雪运动的喜好和性别有关

查看试题解析
10. 已知Sn是等差数列{an}的前n项和，且S₅＜S₆ ， S₆＝S₇ ， S₇＞S₈ ，则（）

A、S₅＜S₉ B、该数列的公差d＜0 C、a₇＝0 D、S₁₁＜0

查看试题解析
11. 盒子里有形状大小都相同的4个球，其中2个红球、2个白球，从中先后不放回地任取2个球，每次取1个．设“两个球颜色相同”为事件A，“两个球颜色不同”为事件B，“第1次取出的是红球”为事件C，“第2次取出的是红球”为事件D．则（）

A、A与B互为对立事件 B、A与C相互独立 C、C与D互斥 D、B与C相互独立

查看试题解析
12. 已知正四棱锥P－ABCD的棱长均为1，O为底面ABCD的中心，M，N分别是棱PA，PB的中点，则（）

A、PA⊥OM B、直线AP与平面OMN所成的角的余弦值为 $\frac{\sqrt{6}}{3}$ C、平面OMN∥平面PCD D、四棱锥P－ABCD的外接球的体积为 $\frac{π}{3}$

查看试题解析

三、填空题

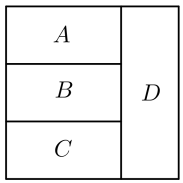
13. 已知数列{an}是等比数列，且a₁＋a₂＋a₃＝1，a₂＋a₃＋a₄＝3，则a₆＋a₇＋a₈＝．

查看试题解析
14. 如图，用4种不同的颜色对图中4个区域涂色，要求每个区域涂1种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有种．

查看试题解析
15. 已知四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 是边长为1的正方形， $P A ⊥$ 平面 $A B C D$ ， $P A = 1$ ，以P为球心 $\sqrt{2}$ 为半径的球面与底面 $A B C D$ 的交线长为．

查看试题解析
16. 甲、乙、丙三人相互做传球训练，第1次由甲将球传出，每次传球时，传球者都等可能的将球传给另外两个人中的任何一人，则5次传球后球在甲手中的概率为.

查看试题解析

四、解答题

17. 已知正整数n≥2，（x＋3）n的展开式为anxn＋ $a_{n - 1} x^{n - 1}$ ＋…＋a₁x＋a₀ ．

(1)、若（x＋3）n的展开式中，各项系数之和比二项式系数之和大992，求n的值；

(2)、若n＝2022，且ak是an，an_－₁ ， …，a₁ ， a₀中的最大值，求正整数k的值．

查看试题解析
18. 已知数列 ${a_{n}}$ 满足a₁＝3，a₂＝5，且 $2 a_{n + 2} = 3 a_{n + 1} - a_{n}$ ， n∈N*．

(1)、设bn＝an_＋₁－an，求证：数列 ${b_{n}}$ 是等比数列；

(2)、若数列{an}满足 $a_{n} \leq m$ （n∈N*），求实数m的取值范围．

查看试题解析
19. 小李准备在某商场租一间商铺开服装店，为了解市场行情，在该商场调查了20家服装店，统计得到了它们的面积x（单位：m²）和日均客流量y（单位：百人）的数据（xi，yi）（i＝1，2，…，20），并计算得 $\sum_{i = 1}^{20} x_{i}$ ＝2400， $\sum_{i = 1}^{20} y_{i}$ ＝220， $\sum_{i = 1} {(x_{i} - \bar{x})}^{2}$ ＝42000， $\sum_{i = 1} (x_{i} - \bar{x}) (y_{i} - \bar{y})$ ＝8400．
附：在线性回归方程ŷ＝ $\hat{a}$ ＋ $\hat{b}$ x中， $\hat{b}$ ＝ $\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a}$ ＝ $\bar{y}$ － $\hat{b}$ $\bar{x}$ ，其中 $\bar{x}$ ， $\bar{y}$ 为样本平均值．

(1)、求y关于x的回归直线方程；

(2)、已知服装店每天的经济效益W＝k $\sqrt{y}$ ＋mx（k＞0，m＞0），该商场现有80~170 m²的商铺出租，根据（1）的结果进行预测，要使单位面积的经济效益Z最高，小李应该租多大面积的商铺?

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{n} = (n + 1) (a_{n} - n)$ $(n \in N^{*})$ ．

(1)、求 $a_{1} ， a_{2}$ ，并求数列 ${a_{n}}$ 的通项公式；

(2)、若数列 ${b_{n}}$ 满足 $b_{n} = {\begin{cases} a_{n} ， 1 \leq n \leq 10 \\ \frac{4}{a_{n} a_{n - 1}} ， n \geq 11 \end{cases}$ ，求数列 ${b_{n}}$ 前 $n$ 项的和 $T_{n}$ ．

查看试题解析
21. 小李下班后驾车回家的路线有两条．路线1经过三个红绿灯路口，每个路口遇到红灯的概率都是 $\frac{1}{3}$ ；路线2经过两个红绿灯路口，第一个路口遇到红灯的概率是 $\frac{1}{2}$ ，第二个路口遇到红灯的概率是 $\frac{2}{3}$ ．假设两条路线全程绿灯时的驾车回家时长相同，且每个红绿灯路口是否遇到红灯相互独立．

(1)、若小李下班后选择路线1驾车回家，求至少遇到一个红灯的概率．

(2)、假设每遇到一个红灯驾车回家时长就会增加1min，为使小李下班后驾车回家时长的累计增加时间（单位：min）的期望最小，小李应选择哪条路线？请说明理由．

查看试题解析
22. 如图，在三棱柱ABC－A₁B₁C₁中，四边形ABB₁A₁为正方形，四边形AA₁C₁C为菱形，且∠AA₁C＝60°，平面AA₁C₁C⊥平面ABB₁A₁ ，点D为棱BB₁的中点．

(1)、求证：AA₁⊥CD；

(2)、棱B₁C₁（除两端点外）上是否存在点M，使得二面角B－A₁M－B₁的余弦值为 $\frac{\sqrt{15}}{5}$ ？若存在，请指出点M的位置；若不存在，请说明理由．

查看试题解析

冰雪运动的喜好	性别		合计
冰雪运动的喜好	男性	女性	合计
喜欢	140	m	140＋m
不喜欢	n	80	80＋n
合计	140＋n	80＋m	220＋m＋n