(鲁教版)2022-2023学年度第一学期六年级数学2.6 有理数的加减混合运算 同步测试
试卷更新日期:2022-08-08 类型:同步测试
一、单选题
-
1. 要使算式的运算结果最大,则“□”内应填入的运算符号为( )A、+ B、- C、× D、÷2. 算式之值为何?( )A、 B、 C、 D、3. 某市冬季中的一天,中午12时的气温是 , 经过6小时气温下降了 , 那么当天18时的气温是( )A、 B、 C、 D、4. 徐志摩的《泰山日出》一文描写了“泰山佛光”壮丽景象.若1月份的泰山山脚平均气温为9℃,山顶平均气温为-2℃,则山脚平均气温与山顶平均气温的温差是( )A、11℃ B、-11℃ C、7℃ D、-7℃5. 一天早晨的气温为-3℃,中午上升了7℃,半夜又下降了8℃,则半夜的气温是( )A、-5℃ B、-4℃ C、4℃ D、-16℃6. 在﹣2□3的“□”中填入一个运算符号使运算结果最小( )A、+ B、﹣ C、× D、÷7. 某日的最高气温为32℃,最低气温为24℃,则这天的最高气温比最低气温高( )A、 B、 C、8℃ D、10℃8. 下面算式与的值相等的是( )A、 B、 C、 D、9. 小云计划户外徒步锻炼,每天有“低强度”“高强度”“休息”三种方案,下表对应了每天不同方案的徒步距离(单位:km).若选择“高强度”要求前一天必须“休息”(第一天可选择“高强度”).则小云5天户外徒步锻炼的最远距离为( )km.
日期
第1天
第2天
第3天
第4天
第5天
低强度
8
6
6
5
4
高强度
12
13
15
12
8
休息
0
0
0
0
0
A、35 B、36 C、37 D、3810. 计算 的结果等于()A、 B、 C、1 D、6二、填空题
-
11. 小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是千米.
t小时
0.2
0.6
0.8
s千米
20
60
80
12. 远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是一位母亲记录孩子出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是天. 13. 甲、乙两施工队分别从两端修一段长度为315米的公路.在施工过程中,甲队曾因技术改进而停工一天,之后加快了施工进度并与乙队共同按期完成任务.下表根据每天工程进度制作而成的.
13. 甲、乙两施工队分别从两端修一段长度为315米的公路.在施工过程中,甲队曾因技术改进而停工一天,之后加快了施工进度并与乙队共同按期完成任务.下表根据每天工程进度制作而成的.施工时间/天
1
2
3
4
5
6
7
8
9
10
累计完成施工量/米
25
50
75
100
115
155
195
235
275
315
甲队技术改进后比技术改进前每天多修路米.
14. 若关于x的多项式 除以 ,所得商恰好为 ,则 .15. 《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”:“粟率五十,粝米三十……”(粟指带壳的谷子,粝米指糙米),其意为:“50单位的粟,可换得30单位的粝米……”问题:有3斗的粟(1斗=10升),若按照此“粟米之法”,则可以换得粝米为 升.三、解答题
-
16. 在1到100这100个数中,任找10个不同的数,使其倒数之和等于1.现已有2个数,为2和6,再写出另外的8个数即可.
17. 在某地区,夏季高山上的温度从山脚起每升高100米平均降低0.8 ℃,已知山脚的温度是24 ℃,山顶的温度是4 ℃,试求这座山的高度.18. 某检修队从A地出发,在东西方向的公路上检修线路.如果规定向东行驶为正,向西行驶为负,这个检修队一天中的行程记录如下(单位:km):-4,+7,-9,+8,+6,-5,-3.若检修队所乘汽车每千米耗油0.3L,问:检修队收工地在何处?从出发到收工共耗油多少升?19. 某冷冻厂的一个冷库的室温是 ℃,现有一批食品需要在 ℃冷藏,如果每小时能降温 ℃,几小时后能降到所要求的温度?20. 请先阅读下列一组内容,然后解答问题:因为:
所以:
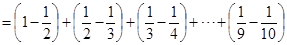
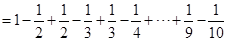
问题:
计算:① ;
②
21. 一个食品加工厂从生产的某标准质量为 的袋装面包中抽取样品10袋,检测每袋的质量是否符合标准,超过或不足的部分用正数或负数来表示,记录如下表:与标准质量的差/g
0
1
3
袋数/袋
1
2
4
2
1
求抽取检测的这批样品的总质量.
22. 某村有6块小麦试验田,每块试验田今年的收成与去年相比的情况如下:(增产为正。减产为负。单位:kg)55,-40,10,-16,27,-5
今年的小麦总产量相比去年情况如何?