2022-2023学年北师大版数学九年级上册第六章 反比例函数 章末检测
试卷更新日期:2022-08-07 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 有下列函数:① ;② ;③ ;④ ;⑤ ;⑥ .其中 是 的反比例函数的有( )A、1个 B、2个 C、3个 D、4个2. 下列关系中,两个量之间为反比例关系的是( )A、正方形的面积S与边长a的关系 B、正方形的周长L与边长a的关系 C、矩形的长为a,宽为20,其面积S与a的关系 D、矩形面积为40,长为a,宽为b,a与b的关系3. 反比例函数y=(k≠0)经过点(-1,4),则下列各点也在这个函数图象上的是( )A、(-1,-4) B、(1,4) C、(-2,-2) D、(2,-2)4. 已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )A、t=40v B、 C、 D、5. 若点 在反比例函数 为常数, 的图象上,则下列有关该函数的说法正确的是( )A、该函数的图象经过点 B、该函数的图象位于第一、三象限 C、 的值随 的增大而增大 D、当 时, 的值随 的增大而增大6. 以下反比例函数图象只位于第二象限的是( )A、 B、 C、 D、7. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、8. 如图,P,Q是反比例函数y=(k>0)图象上的两个点,点Q的横坐标大于点P的横坐标,过点P分别作x轴,y轴的垂线,垂足分别为B,A,过点Q分别作x轴,y轴的垂线,垂足分别为D,C.PB与CQ交于点E,设四边形ACEP的面积为S1 , 四边形BDQE的面积为S2 , 则S1与S2的大小关系为( )
 A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定9. 在同一平面直角坐标系中,函数与的图象可能是( ).A、
A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定9. 在同一平面直角坐标系中,函数与的图象可能是( ).A、 B、
B、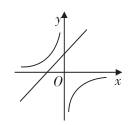 C、
C、 D、
D、 10. 如图,在平面直角坐标系中,点 、 在函数 的图象上.当 时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D . QD交PA于点E . 随着m的增大,四边形ACQE的面积( )
10. 如图,在平面直角坐标系中,点 、 在函数 的图象上.当 时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D . QD交PA于点E . 随着m的增大,四边形ACQE的面积( )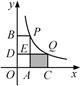 A、减小 B、增大 C、先减小后增大 D、先增大后减小
A、减小 B、增大 C、先减小后增大 D、先增大后减小二、解答题(共7题,共62分)
-
11. 已知反比例函数 的图象过点P(-1,3),求m的值和该反比例函数的表达式.12. 在一个不透明的盒子里,装有四个分别标有数字1、2、3、4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.请用列表法或画树状图法求出点(x,y)落在反比例函数的图象上的概率.13. 商场出售一批进价为2元的贺卡,在市场营销中发现此商品日销售单价x (元)与日销售量y (张) 之间有如下关系:
x/元
3
4
5
6
y /张
20
15
12
10
(1)、根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点;(2)、猜想并确定y关于x的函数解析式,并画出函数图象;(3)、设经营此贺卡的日销售利润为W (元),试求出W关于x的函数解析式,若物价局规定此贺卡的日销售单价最高不能超过10元/张,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?14. 如图,一次函数 与反比例函数 图象的两个交点分别为 , , 轴于点 , 轴于点 . (1)、根据图象直接回答:在第一象限内,当 取何值时,一次函数值大于反比例函数值;(2)、求一次函数的解析式及 的值;(3)、 是线段 上的一点,连接 , ,若 和 的面积相等,求点 的坐标.15. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
(1)、根据图象直接回答:在第一象限内,当 取何值时,一次函数值大于反比例函数值;(2)、求一次函数的解析式及 的值;(3)、 是线段 上的一点,连接 , ,若 和 的面积相等,求点 的坐标.15. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)、每月产销量y(个)与销售单价x(元)之间的函数关系式为 ▲ ;从上表可知.每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;(2)、若每个玩具的固定成本为30元,求它的销售单价是多少元?(3)、若该厂这种玩具的月产销量不超过400个,求此时销售单价是多少元?16. 为了探索函数y=x+ (x>0)的图象与性质,我们参照学习函数的过程与方法.列表:
x
…
1
2
3
4
5
…
y
…
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图1所示:
 (1)、如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点(x1 , y1),(x2 , y2)在函数图象上,结合表格和函数图象,回答下列问题:
(1)、如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点(x1 , y1),(x2 , y2)在函数图象上,结合表格和函数图象,回答下列问题:若0<x1<x2≤1,则y1y2;若1<x1<x2 , 则y1y2;
若x1•x2=1,则y1y2(填“>”,“=”或“<”).
(3)、某农户要建造一个图2所示的长方体形无盖水池,其底面积为1平方米,深为1米.已知底面造价为1千元/平方米,侧面造价为0.5千元/平方米.设水池底面一边的长为x米,水池总造价为y千元.①请写出y与x的函数关系式;
②若该农户预算不超过3.5千元,请直接写出水池底面一边的长x的取值范围.
17. 如图1所示,已知 图象上一点 轴于点 ,点 ,动点 是 轴正半轴点 上方的点,动点 在射线AP上,过点 作AB的垂线,交射线AP于点 ,交直线MN于点 ,连结AQ,取AQ的中点 .
 (1)、如图2,连结BP,求 的面积;(2)、当点 在线段BD上时,若四边形BQNC是菱形,面积为 .
(1)、如图2,连结BP,求 的面积;(2)、当点 在线段BD上时,若四边形BQNC是菱形,面积为 .①求此时点Q,P的坐标;
②此时在y轴上找到一点E,求使|EQ-EP|最大时的点E的坐标.