2022-2023学年北师大版数学九年级上册6.3反比例函数的应用 同步练习
试卷更新日期：2022-08-07 类型：同步测试
一、单选题（每题3分，共30分）
-
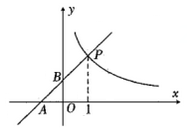
1. 如图，直线y=x+2与反比例函 的图象在第一象限交于点P.若 ，则k的值为（ ）
A、6 B、8 C、10 D、122. 如图所示的是反比例函数和一次函数的图象，则下列结论正确的是（ ）
A、反比例函数的解析式是 B、一次函数的解析式为 C、当时， D、若 ， 则3. 函数与在同一坐标系中的图象可能是A、
B、
C、
D、
4. 函数y＝ 和y＝ 在第一象限内的图象如图，点P是y＝ 的图象上一动点，PC⊥x轴于点C，交y＝ 的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA＝ AP．其中所有正确结论的序号是（ ）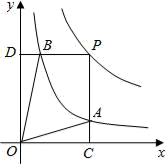
A、①②③ B、②③④ C、①③④ D、①②④5. 已知蓄电池的电压为定值．使用电池时，电流I（A）与电阻R（Ω）是反比例函数关系，图象如图所示．如果以此蓄电池为电源的电器的限制电流不能超过3A，那么电器的可变电阻R（Ω）应控制在（ ）
A、R≥1 B、0＜R≤2 C、R≥2 D、0＜R≤16. 小明乘车从县城到怀化，行车的速度和行车时间之间函数图是（ ）A、
B、
C、
D、
7. 为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产进行治污改造，其月利润y（万元）与月份x之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的一部分，下列选项正确的是（ ）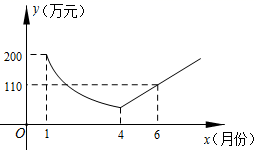
A、4月份的利润为50万元 B、治污改造完成后每月利润比前一个月增加30万元 C、治污改造完成前后共有3个月的利润低于100万元 D、8月份该厂利润达到200万元8. 一辆汽车匀速通过某段公路，所需时间（h）与行驶速度 （km/h）满足函数关系 点 ，其图象为如图所示的一段双曲线，端点为 和 ，若行驶速度不得超过60 km/h，则汽车通过该路段最少需要（ ）
A、 分钟 B、40分钟 C、60分钟 D、 分钟9. A，B两城间的距离为15千米，一人行路的平均速度每小时不少于3千米，也不多于5千米，则表示此人由A到B的行路速度x（千米/小时）与所用时间y（小时）的关系y= 的函数图象是（ ）A、
B、
C、
D、
10. 小明学习了物理中的杠杆平衡原理发现：阻力 阻力臂 动力 动力臂．现已知某一杠杆的阻力和阻力臂分别为2400N和1m，则动力 （单位：N）关于动力臂 （单位：m）的函数图象大致是（ ）A、
B、
C、
D、
二、填空题（每题3分，共18分）
-
11. 正比例函数和反比例函数的图象都经过点A(-1， 2)，若 ， 则x的取值范围是 ．12. 已知：如图，直线与双曲线在第一象限交于点 ， 则k的值为；当时， ． （填“＞”或“＜”）
13. 如图，边长为1的正方形拼成的矩形如图摆放在直角坐标系里，A，B，C，D是格点。反比例函数y= (x>0，k>0)的图象经过格点A并交CB于点E。若四边形AECD的面积为6.4，则k的值为 。
14. 为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为6mg．研究表明当每立方米空气中含药量低于1.2mg时，对人体方能无毒害作用，那么从消毒开始，至少需要经过分钟后，学生才能回到教室．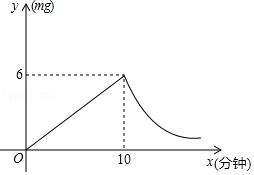
15. 如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y1= （x＞0）的图象上，顶点B在函数y2= （x＞0）的图象上，∠ABO=30°，则 = ．
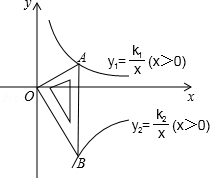16. 某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y（毫克）与时间t（小时）之间的函数关系近似满足如图所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为.
三、解答题（共8题，共52分）
-
17. 已知反比例函数 的图象与正比例函数 的图象交于点 ，求这个反比例函数的表达式，并在同一平面直角坐标系内，画出这两个函数的图象．18. 如图，一次函数 的函数图象与反比例函数 的图象交于点A（2，3）和点B，与x轴相交于点C（8，0）.求这两个函数的解析式；
19. 已知近视眼镜的度数y（度）与镜片焦距x（米）成反比例关系，且400度近视眼镜镜片的焦距为0.25米．小慧原来戴400度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为0.4米的眼镜了，求小慧所戴眼镜的度数降低了多少度．20. 如图是某游乐园“水上滑梯”的侧面示意图，其中BD段可看成双曲线 的一部分，矩形OABC是向上攀爬的阶梯部分．以O为中心建立平面直角坐标系，使点A和点C分别落在x轴和y轴的正半轴上．已知OC=5米，入口平台BC=1.8米，滑梯的出口D点到水面的距离DE为0.75米（O、A、E在一条直线上）．求B、D之间的水平距离AE的长．
21. 如图，一次函数的图象与反比例函数的图象相交于A、B两点，其中点A的坐标为(-1，4)，点B的坐标为(4，n)．
(1)、求这两个函数的表达式；(2)、点P在线段AB上，且 ， 求点P的坐标．22. 如图，在矩形ABCD中，已知点A（2，1），且AB＝4，AD＝3，把矩形ABCD的内部及边上，横、纵坐标均为整数的点称为靓点，反比例函数y＝（x＞0）的图象为曲线L．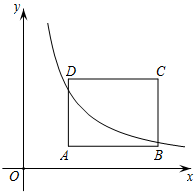
(1)、若曲线L过AB的中点．①求k的值．
②求该曲线L下方（包括边界）的靓点坐标．
(2)、若分布在曲线L上方与下方的靓点个数相同，求k的取值范围．23. 如图，某校劳动小组计划利用已有的一堵长为6m的墙，用篱笆围成一个面积为12m2的矩形劳动基地ABCD，边AD的长不超过墙的长度，在BC边上开设宽为1m的门EF（门不需要篱笆）．设AB的长为x（m），BC的长为y（m）．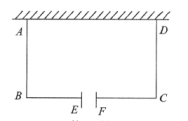
(1)、求y关于x的函数表达式．(2)、若围成矩形劳动基地ABCD三边的篱笆总长为10m，求AB和BC的长度．(3)、若AB和BC的长都是整数（单位：m），且围成矩形劳动基地ABCD三边的篱笆总长小于10m，请直接写出所有满足条件的围建方案．24. 某小组进行漂洗实验，每次漂洗的衣服量和添加洗衣粉量固定不变实验发现，当每次漂洗用水量v（升）一定时，衣服中残留的洗衣粉量y（克）与漂洗次数x（次）满足y=（k为常数），已知当使用5升水，漂洗1次后，衣服中残留洗衣粉2克．(1)、求k的值．(2)、如果每次用水5升，要求漂洗后残留的洗衣粉量小于0.8克，求至少漂洗多少次？(3)、现将20升水等分成x次（x>1）漂洗，要使残留的洗衣粉量降到0.5克，求每次漂洗用水多少升？