2022-2023学年北师大版数学九年级上册6.2反比例函数的图象与性质 同步练习
试卷更新日期:2022-08-07 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 反比例函数y=是经过点(2,3),那么这个反比例函数的图象应在( )A、第一、二象限 B、第一、三象限 C、第二,三象限 D、第二、四象限2. 在同一平面直角坐标系中,函数y=kx+k与y=(k≠0)的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知反比例函数 , 则下列描述正确的是( )A、图象位于第一、三象限 B、图象必经过点 C、图象必经过点 D、y随x的增大而减小4. 对于反比例函数 , ①这个函数图象的两个分支分别位于第二、四象限,②这个函数的图象既是轴对称图形又是中心对称图形,③点不在这个函数图象上,④若点和点在该函数图象上,则.上述四个判断中,不正确的个数是( )A、3 B、2 C、1 D、05. 如图,反比例函数 图象的对称轴的条数是( )
3. 已知反比例函数 , 则下列描述正确的是( )A、图象位于第一、三象限 B、图象必经过点 C、图象必经过点 D、y随x的增大而减小4. 对于反比例函数 , ①这个函数图象的两个分支分别位于第二、四象限,②这个函数的图象既是轴对称图形又是中心对称图形,③点不在这个函数图象上,④若点和点在该函数图象上,则.上述四个判断中,不正确的个数是( )A、3 B、2 C、1 D、05. 如图,反比例函数 图象的对称轴的条数是( ) A、0 B、1 C、2 D、36. 在反比例函数 的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )A、-1 B、0 C、1 D、27. 下列函数中,当 时,y随x的增大而增大的是( )A、 B、 C、 D、8. 若点 , , 在双曲线 上,则 , , 的大小关系是( )A、 B、 C、 D、9. 在平面直角坐标系中,点P是y轴正半轴上的任意一点,过点P作x轴的平行线,分别与反比例函数y和y的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )A、10 B、12 C、14 D、2810. 如图,A,B是反比例函数 图象上的两点,分别过点A,B作x轴,y轴的垂线,构成图中的三个相邻且不重叠的小矩形 , , ,已知 , 的值为( )
A、0 B、1 C、2 D、36. 在反比例函数 的图象的每一条曲线上,y随x的增大而增大,则k的值可以是( )A、-1 B、0 C、1 D、27. 下列函数中,当 时,y随x的增大而增大的是( )A、 B、 C、 D、8. 若点 , , 在双曲线 上,则 , , 的大小关系是( )A、 B、 C、 D、9. 在平面直角坐标系中,点P是y轴正半轴上的任意一点,过点P作x轴的平行线,分别与反比例函数y和y的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为( )A、10 B、12 C、14 D、2810. 如图,A,B是反比例函数 图象上的两点,分别过点A,B作x轴,y轴的垂线,构成图中的三个相邻且不重叠的小矩形 , , ,已知 , 的值为( ) A、16 B、10 C、8 D、5
A、16 B、10 C、8 D、5二、填空题(每题3分,共18分)
-
11. 若双曲线 在第二、四象限,则直线y=kx-2不经过第象限.12. 若反比例函数y=的图象经过点(-2,6)和(4,m),则m= .13. 直线y=kx与双曲线y= 交于A(x1 , y1)、B(x2 , y2)两点,则x1y2﹣3x2y1的值为.14. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 .
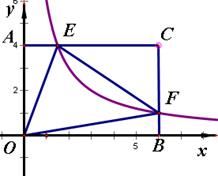
 15. 如图,双曲线 经过Rt 斜边上的中点A,与BC交于点D, ,则 .
15. 如图,双曲线 经过Rt 斜边上的中点A,与BC交于点D, ,则 .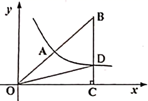 16. 如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,4)也在此函数的图象上,则a= .
16. 如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,4)也在此函数的图象上,则a= .
三、解答题(共8题,共52分)
-
17. 在平面直角坐标系中,画出函数 的图象.
 18. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值.
18. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值. 19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. (1, )是反比例函数图象上的一点,直线AC经过坐标原点且与反比例函数图象的另一支交于点C , 求C的坐标及反比例函数的表达式.21. 已知反比例函数 , 其中 , 且 , .(1)、若随的增大而增大,则的取值范围是;(2)、若该函数的最大值与最小值的差是 , 求的值.22. 如图,点A在反比例函数 的图象位于第一象限的分支上,过点A作AB⊥y轴于点B,S△AOB=2.
19. 已知函数 , ,当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.20. (1, )是反比例函数图象上的一点,直线AC经过坐标原点且与反比例函数图象的另一支交于点C , 求C的坐标及反比例函数的表达式.21. 已知反比例函数 , 其中 , 且 , .(1)、若随的增大而增大,则的取值范围是;(2)、若该函数的最大值与最小值的差是 , 求的值.22. 如图,点A在反比例函数 的图象位于第一象限的分支上,过点A作AB⊥y轴于点B,S△AOB=2.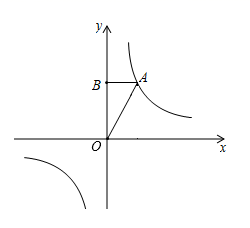 (1)、求该反比例函数的表达式,(2)、若P(x1 , y1)、Q(x2 , y2)是反比例函数 图象上的两点,且x1 x2 , y1 y2 , 指出点P、Q各位于哪个象限,并简要说明理由.
(1)、求该反比例函数的表达式,(2)、若P(x1 , y1)、Q(x2 , y2)是反比例函数 图象上的两点,且x1 x2 , y1 y2 , 指出点P、Q各位于哪个象限,并简要说明理由.