2022-2023学年北师大版数学九年级上册第四章图形的相似章末检测

试卷更新日期：2022-08-07 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列各组中的四条线段成比例的是（）

A、1，1，2，3 B、1，2，3，4 C、2，3，4，5 D、2，3，6，9

查看试题解析
2. 若 $3 a = 5 b (b \neq 0)$ ，则下列各式一定成立的是（）

A、 $\frac{a}{b} = \frac{3}{5}$ B、 $\frac{a}{b} = \frac{5}{3}$ C、 $\frac{a}{3} = \frac{b}{5}$ D、 $\frac{a + 1}{b} = \frac{4}{5}$

查看试题解析
3. 如果 $\frac{a}{b} = \frac{2}{3}$ ，且 $b$ 是 $a$ 和 $c$ 的比例中项，那么 $\frac{b}{c}$ 等于（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 如图， $A B / / C D / / E F$ ，若 $B F = 3 D F$ ，则 $\frac{A C}{C E}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、3

查看试题解析
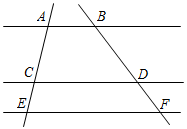5. 下列命题中，是真命题的是（）

A、正方形都相似 B、矩形都相似 C、等腰三角形都相似 D、直角三角形都相似

查看试题解析
6. 两个相似多边形的一组对应边分别是3cm和4.5cm，如果它们的周长之和是80cm，那么较大的多边形的周长是（）

A、16cm B、32cm C、48cm D、52cm

查看试题解析
7. 如果点 $P$ 是线段AB的黄金分割点，且 $A P < B P$ ，那么 $\frac{A P}{B P}$ 的值等于（）

A、 $\frac{\sqrt{5}}{2} + 1$ B、 $\frac{\sqrt{5}}{2} - 1$ C、 $\frac{\sqrt{5} + 1}{2}$ D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 如图，在△ABC中，DE∥BC， $\frac{D E}{B C}$ ＝ $\frac{1}{3}$ ，则下列结论中正确的是（）

A、 $\frac{A E}{E C} = \frac{1}{3}$ B、 $\frac{A D}{A B} = \frac{1}{2}$ C、 $\frac{Δ A D E 的周长}{Δ A B C 的周长} = \frac{1}{3}$ D、 $\frac{Δ A D E 的面积}{Δ A B C 的面积} = \frac{1}{3}$

查看试题解析
9. $△$ ABC~ $△ A^{'} B^{'} C^{'}$ ，若AB： $A^{'} B^{'}$ =3：4，则 $S_{△ A B C} ： S_{△ A^{'} B^{'} C^{'}}$ =（）

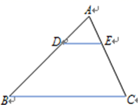A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{16}{9}$ D、 $\frac{9}{16}$

查看试题解析
10. 如图，在平面直角坐标系中，△OAB的顶点O在坐标原点，顶点A，B的坐标分别为（－2，－1），（－1.5，0）．△OCD与△OAB位似，位似中心是原点O，若点D的坐标为（4.5，0），则点C的坐标为（）

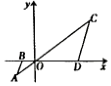A、（6，3） B、（－6，－3） C、（4，2） D、（－4，－2）

查看试题解析

二、填空题（每题4分，共24分）

11. 如果 $\frac{x}{2} = \frac{y}{3} = \frac{z}{5} \neq 0$ ，那么 $\frac{y - x}{z} =$ ．

查看试题解析
12. 如图，两条直线被三条平行直线所截，DE=4，EF=6，AB=2，则AC=.

查看试题解析
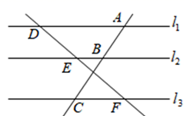13. 如果四边形ABCD的四条边长分别为54cm、48cm、45cm、63cm，另一个和它相似的四边形的最长边长为21cm，那么这个四边形的最短边的长度为.

查看试题解析
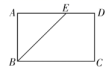14. 我们把宽与长的比为黄金比 $(\frac{\sqrt{5} - 1}{2})$ 的矩形称为黄金矩形，如图，在黄金矩形 $A B C D$ 中， $A B < B C$ ， $B C = 2$ ， $∠ A B C$ 的平分线交 $A D$ 边于点 $E$ ，则 $D E$ 的长为．

查看试题解析
15. 如图，在直角∆ABC中，∠C＝90°，AC＝8，BC＝6，点M从点C出发沿线段CA向点A移动，连接BM，MN⟂BM交边AB于点N．若CM＝2，那么线段AN＝；当点M从点C移动到AC的中点时，则点N的运动过程中路径长为。

查看试题解析
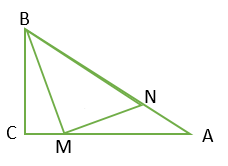16. 某户外遮阳棚如图1，其截面结构示意图如图2所示.支撑柱AB上地面，AB=120 $\sqrt{5}$ cm，Р是支撑柱AB上一动点，伞杆CP可绕着中点E旋转，CD=CP=40 $\sqrt{15}$ cm，斜拉杆AE可绕点A旋转，AE= $\frac{1}{2}$ CP．若∠APE=30°，则BP=cm；伞展开长 PD==300cm，若A，C，D在同一条直线上，某时太阳光线恰好与地面垂直，则PD落到地面的阴影长为cm.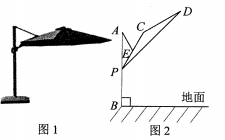

查看试题解析

三、解答题（共8题，共66分）

17. 已知a、b、c为三角形ABC的三边长，且 $a + b + c = 36$ ， $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，求三角形ABC三边的长．

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立平面直角坐标系.

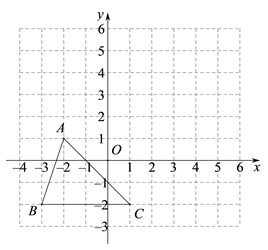(1)、以原点O为位似中心，将△ABC放大，使变换后得到的△A₁B₁C₁与△ABC对应边的比为2∶1，请在给定的网格内画出△A₁B₁C₁.

(2)、设点P（a，b）为△ABC内一点，请直接写出依上述变换后点P在△A₁B₁C₁内的对应点P₁的坐标是.

查看试题解析
19. 如图，在5×5的方格纸中，已知格点 $△$ ABC，请按要求画图.

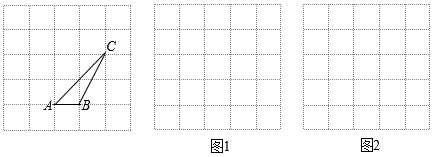(1)、在图1画一个格点 $△$ DEF，使 $△$ DEF与 $△$ ABC相似，且 $△$ DEF与 $△$ ABC的周长比是2.

(2)、在图2画一个格点 $△$ MNL，使 $△$ MNL与 $△$ ABC相似，且 $△$ MNL与 $△$ ABC的面积比是2.

查看试题解析
20. 如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示．

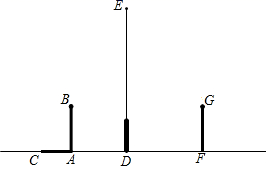(1)、请你通过画图确定灯泡所在的位置．

(2)、如果小明的身高AB＝1.6m，他的影子长AC＝1.4m，且他到路灯的距离AD＝2.1m，求灯泡的高．

查看试题解析
21. 如图，在△ABC中，AD是BC边上的中线，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F.

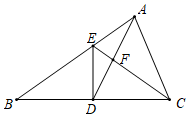(1)、求证：△ABC∽△FCD；

(2)、过点A作AM⊥BC于点M，求DE：AM的值；

(3)、若S_△_FCD=5，BC=10，求DE的长.

查看试题解析
22. 梅涅劳斯定理
梅涅劳斯（ $M e n e l a u s$ ）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：

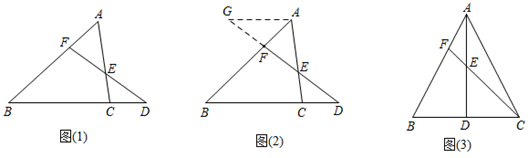
如图（1），如果一条直线与 $Δ A B C$ 的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有 $\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1$ ．

下面是利用相似三角形的有关知识证明该定理的部分过程：

证明：如图（2），过点A作 $A G // B C$ ，交DF的延长线于点G，则有 $\frac{A F}{F B} = \frac{A G}{B D}$ ．

任务：

(1)、请你将上述材料中的剩余的证明过程补充完整；

(2)、如图（3），在 $Δ A B C$ 中， $A B = A C = 13$ ， $B C = 10$ ，点D为BC的中点，点F在AB上，且 $B F = 2 A F$ ，CF与AD交于点E，则 $A E =$ ．

查看试题解析
23. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ cm， $B C = 3$ cm，点P由点B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC方向向点C匀速运动，速度为1cm/s，连接PQ.设运动的时间为t（s），其中 $0 < t < 4$ .解答下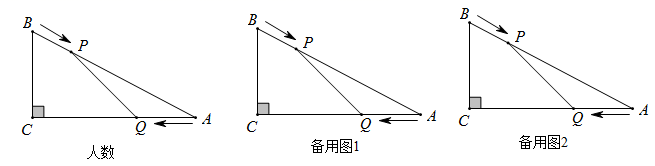列问题：

(1)、AP= ， AQ=；（用含t的代数式表示）

(2)、当t为何值时， $Δ A P Q$ ∽ $Δ A B C$ ；

(3)、当P、Q在运动过程中， $Δ A P Q$ 能否成为等腰三角形？若能，求出此时t的值；若不能，请说明理由.

查看试题解析
24. 如图，用四根木条钉成矩形框 $A B C D$ ，把边 $B C$ 固定在地面上，向右推动矩形框，矩形框的形状会发生改变（四边形具有不稳定性）.

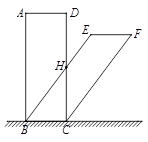(1)、通过观察分析，我们发现图中线段存在等量关系，如线段 $E B$ 由 $A B$ 旋转得到，所以 $E B = A B$ .我们还可以得到 $F C$ = ， $E F$ = ；

(2)、进一步观察，我们还会发现 $E F$ ∥ $A D$ ，请证明这一结论；

(3)、已知 $B C = 30 c m ， D C = 80 c m$ ，若 $B E$ 恰好经过原矩形 $D C$ 边的中点 $H$ ，求 $E F$ 与 $B C$ 之间的距离.

查看试题解析

2022-2023学年北师大版数学九年级上册第四章 图形的相似 章末检测

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022-2023学年北师大版数学九年级上册第四章图形的相似章末检测