2022-2023学年北师大版数学九年级上册4.7相似三角形的性质 同步练习
试卷更新日期：2022-08-07 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 已知 ，且相似比为 ，则 与 的周长比为（ ）A、 B、 C、 D、2. 如图，已知△ABC∽△ACP，∠A＝70°，∠APC＝65°，则∠B的度数为（ ）
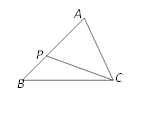A、45° B、50° C、55° D、60°3. 已知ABO∽DEO，且BO：EO＝1：3，则△ABO与△DEO的面积比是（ ）
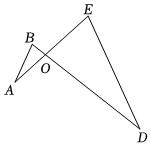A、1：3 B、3：1 C、1：9 D、9：14. 如图，在 的方格纸中，每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形.点E是格点四边形ABCD的AB边上一动点，连接ED，EC，若格点 与 相似，则 的长为（ ）
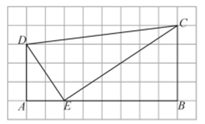A、 B、 C、 或 D、 或5. 如果两个相似三角形的周长比为1：4，那么这两个三角形的对应中线的比为（ ）A、1：2 B、1：4 C、1：8 D、1：166. 如果两个相似三角形的周长比为 ， 那么它们的对应角平分线的比为（ ）A、 B、 C、 D、7. 如果两个相似三角形的面积比是4：9，则它们对应边上的高之比为（ ）A、4：9 B、16：81 C、2：3 D、3：28. 如图，已知 ， 若 ， ， ， 则AC的长是（ ）
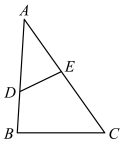A、12 B、13 C、14 D、159. 如图，△ABC∽△ADE，且BC＝2DE，则S四边形BEDC：S△ABC的值为（ ）
A、1：4 B、3：4 C、2：3 D、1：210. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形，A、B、C的纸片的面积分别为S1、S2、S3 ， （S1与S2 ， S2与S3的相似比相同），相邻纸片之间互不重叠也无缝隙，若S1＞S2＞S3 ， 则这个矩形的面积一定可以表示为（ ）
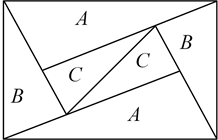A、4S1 B、6S2 C、4S2+3S3 D、3S1+4S3二、填空题（每题3分，共18分）
-
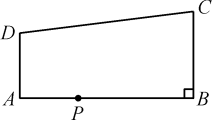
11. 如果两个相似三角形的周长比是1︰4，那么它们的面积比是.12. 若 ， ， 的面积为 ，则 的面积为 .13. 若将△ABC的各边都扩大为原来的2倍，则该三角形的周长会扩大为原来的倍.14. 若D为中边上一点，且EDBC交于E， ， 若与的相似比为 ， 则.15. 如图所示，已知AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC相似，则AP= ．
16. 如果两个相似三角形的面积比为1：4，其中较大三角形的周长为18，那么较小三角形的周长是 ．三、解答题（共8题，共52分）
-
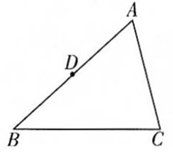
17. 尺规作图：已知点D为△ABC的边AB的中点，用尺规在△ABC的边AC上找一点E，使 （保留作图痕迹，不写作法）.
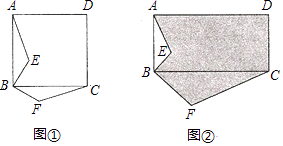
18. 已知△ABC∽△DEF，且DE＝2 cm，AB＝4 cm，BC＝5 cm，CA＝6 cm，求△DEF的周长.19. 如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？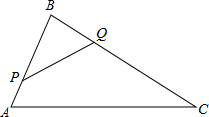
20.问题探究：如图①，四边形 ABCD是正方形，BE⊥BF，BE=BF，求证：△ABE≌△CBF；
方法拓展：如图②，ABCD是矩形，BC=2AB，BF⊥BE，BF=2BE，若矩形ABCD的面积为40，△ABE的面积为4，求阴影部分图形的面积．
21. 如图，AD和BC相交于点E，AC∥BD，点F在CD上，AC＝4，BD＝6， ，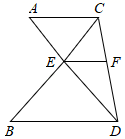
(1)、求EF的长；(2)、已知S△CBD＝25，求△CEF的面积．22. 如图，在平行四边形 中， 为对角线 上一点， 交 于点 ，交 的延长线于点 .
(1)、请找出一对相似的三角形并证明；(2)、若 ，求 的值.23. 如图，在 ABCD中，点E在BC边上，点F在DC的延长线上，且∠DAE=∠F．
(1)、求证：△ABE∽△ECF；(2)、若AB=5，AD=8，BE=2，求FC的长．24. 如图，在△ABC中，∠B＝90°，AB＝6cm ， BC＝8cm ． 点P从点A开始沿边AB向点B以每秒1cm的速度移动，点Q从点B开始沿边BC向点C以每秒2cm的速度移动，点P ， Q分别从点A ， B同时出发，且当一点到达终点时，另一点也停止运动．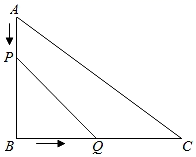
(1)、经过多少秒，可使PBQ的面积等于8cm2？(2)、经过多少秒，△ABC与△PBQ相似？(3)、线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能，请说明理由．