2022-2023学年北师大版数学九年级上册4.6利用相似三角形测高 同步练习
试卷更新日期：2022-08-07 类型：同步测试
一、单选题（每题3分，共30分）
-
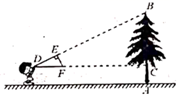
1. 如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边 cm， cm，测得边DF离地面的高度 m， m，则树高AB为（ ）
A、4m B、5m C、5.5m D、6.5m2. 小莹同学的身高为1.6米，某一时刻她在阳光下的影长为3.2米，与她邻近的一棵树的影长为8米，则这棵树的高为（ ）A、3.2米 B、3米 C、4米 D、4.2米3. 如图，图1是装了液体的高脚杯，加入一些液体后如图2所示，则此时液面AB为（ ）
A、5.6cm B、6.4cm C、8cm D、10cm4. 如图，身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时，发现自己在地面上的影子CE的长是2米，则路灯AB的高为（ ）
A、5米 B、6.4米 C、8米 D、10米5. 如图，利用标杆BE测量建筑物的高度，已知标杆BE高1.5m，测得AB＝2m，BC＝12m，则建筑物CD的高度为（ ）
A、10.5m B、10m C、9m D、11m6. 如图所示为某种型号的台灯的横截面图，已知台灯灯柱AB的长为30cm，且与水平桌面垂直，灯臂AC的长为10cm，灯头的横截面CEF为直角三角形，当灯臂AC与灯柱AB垂直时，沿CE边射出的光线刚好射到底座B点.若不考虑其他因素，则该台灯在桌面可照亮的宽度BD的长为（ ）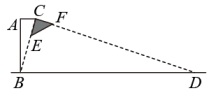
A、90cm B、100cm C、 D、7. 如图，小芳和爸爸正在散步，爸爸身高1.8m，他在地面上的影长为2.1m．若小芳身高只有1.2m，则她的影长为（ ）
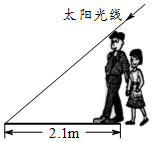A、1.2m B、1.4m C、1.6m D、1.8m8. 如图，小颖把一面镜子水平放置在离树底（点B）8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢（点A），已知 米，小颖目高 米，则树的高度AB为（ ）
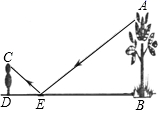A、3.2米 B、4.8米 C、8米 D、20米9. 如图所示，为了测量文昌塔AB的高度，数学兴趣小组根据光的反射定理（图中 ），把一面镜子放在点C处，然后观测者沿着直线BC后退到点D.这时恰好在镜子里看到塔顶A，此时量得 ， ，观测者目高 ，则塔AB的高度为（ ）
A、35m B、36m C、37m D、38m10. 如图所示，某同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时尺子的刻度为12cm，已知臂长60cm，则电线杆的高度为（ ）
A、2.4m B、24m C、0.6m D、6m二、填空题（每题3分，共18分）
-
11. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm．他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像．蜡烛应放在距离纸筒 cm的地方．
12. 如图，某时刻阳光通过窗口AB照射到室内，在地面上留下4米宽的“亮区”DE，光线与地面所成的角（如∠BEC）的正切值是 ， 那么窗口的高AB等于米．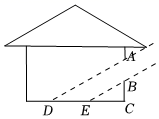
13. 如图，在测量旗杆高度的数学活动中，某同学在地面放了一个平面镜C，然后向后退，直到他刚好在镜子中看到旗杆的顶部A．如果他的眼睛到地面的距离ED＝1.6m，同时量得他到平面镜C的距离DC＝2m，平面镜C到旗杆的底部B的距离CB＝15m，那么旗杆高度AB＝m．
14. 榆社文峰塔位于晋中市榆社县城东南的巽山之上，建于清代康熙年间，文峰塔不仅构思奇特，工艺精巧，而且选址巧妙，寓意深远．老师希望同学们利用所学过的知识测量文峰塔的高度，为此数学兴趣小组的同学们设计了如图所示的测量示意图，并测出竹竿长2米，在太阳光下，它的影长为1.5米，同一时刻，测得文峰塔的影长约为28.5米，请根据测量数据计算出文峰塔的高度约为米．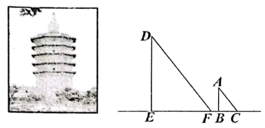
15. 《九章算术》是我国古代数学名著，书中有如下问题：“今有井径五尺，不知其深，立三尺木于井上，从木末望水岸，入径五寸．问井深几何？”意思是：如图，井径尺，立木高尺，寸尺，则井深为尺．
16. 公共自行车车桩的截面示意图如图所示，AB⊥AD，AD⊥DC，点B、C在EF上，EF∥HG，EH⊥HG，AB＝80cm，AD＝24cm，BC＝25cm，EH＝4cm．
(1)、点C到AB的距离为 cm．(2)、点A到地面的距离为 cm．三、解答题（共8题，共52分）
-
17. 如图，在甲、乙两座楼正中间有一堵院墙，小明站在甲楼某层窗口前，同时小光站在乙楼某层窗口前观察这堵墙，小明视线所及位置如图所示，小光视线恰好落在甲楼底部.已知墙的高度为5米，两栋楼的间距为100米，小明视线所及位置到墙的距离为10米.
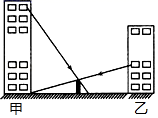(1)、请根据题意画出平面图形，并标上相应字母.(2)、求甲、乙两人的观测点到地面高度的距离差.18. 下表是小明填写的实践报告的部分内容，请你借助小明的测量数据，计算小河的宽度AB.题目
测量小河的宽度
测量目标示意图
相关数据
BCDE，BC＝1m，DE＝1.5m，BD＝5m
19. 如图，已知小华、小强的身高都是1.6m，小华、小强之间的水平距离BC为14m，在同一盏路灯下，小华的影长AB=4m，小强的影长CD=3m，求这盏路灯OK的高度.
20. 王老师要装修自己带阁楼的新居（下图为新居剖面图），在建造客厅到阁楼的楼梯 时，为避免上楼时墙角 碰头，设计墙角 到楼梯的竖直距离 为 ，他量得客厅高 ，楼梯洞口宽 ，阁楼阳台宽 .请你帮助王老师解决问题：要使墙角 到楼梯的竖直距离 为 ，楼梯底端 到墙角 的距离 是多少米？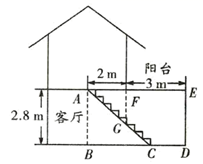
21. 我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图，此时小亮的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直，已知装饰面的高度AD为0.66米.
(1)、求证：；(2)、求装饰画顶部到墙壁的距离DC（精确到0.01米）.22. 为了测量学校旗杆的高度AB，数学兴趣小组带着标杆和皮尺来到操场进行测量，测 量方案如下：如图，首先，小红在C处放置一平面镜，她从点C沿BC后退，当退行1.8米到D处时，恰好在镜子中看到旗杆顶点A的像，此时测得小红眼睛到地面的距离ED为1.5米；然后，小明在F 处竖立了一根高1.6米的标杆FG，发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上，此时测得FH为2.4米，DF为3.3米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上.
(1)、直接写出 ；(2)、请根据以上所测数据，计算学校旗杆AB的高度.23. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量．他们在旗杆底部所在的平地上，放置一个平面镜E来测量学校旗杆的高度，当镜子中心与旗杆的距离EB＝20米，镜子中心与测量者的距离ED＝2米时，测量者刚好从镜子中看到旗杆的顶端点A．已知测量者的身高为1.6米，测量者的眼睛距地面的高度为1.5米，求学校旗杆的高度是多少米．
(1)、在计算过程中C，D之间的距离应是米．(2)、根据以上测量结果，请你帮助“综合与实践”小组求出学校旗杆AB的高度．(3)、该“综合与实践”小组在定制方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）24. 学习了相似三角形相关知识后，小明和同学们想利用“标杆”测量大楼的高度．如图，小明站立在地面点F处，他的同学在点B处竖立“标杆”AB ， 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上（点F、B、D也在一条直线上）．已知小明的身高EF＝1.5米，“标杆”AB＝2.5米，又BD＝23米，FB＝2米．
(1)、求大楼的高度CD为多少米（CD垂直地面BD）？(2)、小明站在原来的位置，同学们通过移动标杆，可以用同样的方法测得楼CD上点G的高度GD＝11.5米，那么相对于第一次测量，标杆AB应该向大楼方向移动多少米？