2022-2023学年北师大版数学九年级上册4.4-4.5同步练习
试卷更新日期:2022-08-07 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列格点三角形中,与右侧已知格点相似的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列图形,一定相似的是( )A、两个直角三角形 B、两个等腰三角形 C、两个等边三角形 D、两个菱形3. 若点C为线段AB的黄金分割点,AB=8,则AC的长是( )A、-4 B、9- C、-3或9- D、-4或12-4. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )
2. 下列图形,一定相似的是( )A、两个直角三角形 B、两个等腰三角形 C、两个等边三角形 D、两个菱形3. 若点C为线段AB的黄金分割点,AB=8,则AC的长是( )A、-4 B、9- C、-3或9- D、-4或12-4. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )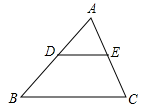 A、8 B、12 C、14 D、165. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )
A、8 B、12 C、14 D、165. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )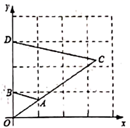 A、 B、 C、 D、6. 某品牌汽车将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58米,倒车镜到车尾部分的水平距离较长,则该车车身总长约为( )米.
A、 B、 C、 D、6. 某品牌汽车将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58米,倒车镜到车尾部分的水平距离较长,则该车车身总长约为( )米. A、4.14 B、2.56 C、6.70 D、3.827. 如图,D为△ABC中AC边上一点,则添加下列条件不能判定△ABC∽△BDC的是( )
A、4.14 B、2.56 C、6.70 D、3.827. 如图,D为△ABC中AC边上一点,则添加下列条件不能判定△ABC∽△BDC的是( ) A、 B、 C、∠ABC=∠BDC D、∠A=∠CBD8. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )
A、 B、 C、∠ABC=∠BDC D、∠A=∠CBD8. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )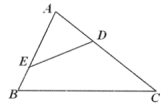 A、 B、 C、 D、9. 如图,要判定与相似,欲添加一个条件,下列可行的条件有
A、 B、 C、 D、9. 如图,要判定与相似,欲添加一个条件,下列可行的条件有( 1 );(2);(3);(4);(5).
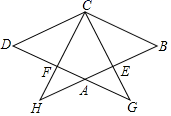
 A、1个 B、2个 C、3个 D、4个10. 如图,E是的边的延长线上一点,连接交于F,则图中共有相似三角形( )
A、1个 B、2个 C、3个 D、4个10. 如图,E是的边的延长线上一点,连接交于F,则图中共有相似三角形( ) A、4对 B、3对 C、2对 D、1对
A、4对 B、3对 C、2对 D、1对二、填空题(每题3分,共18分)
-
11. 如果的值是黄金分割数,那么的值为 .12. 如图,∠1=∠2,请添加一个条件 , 使△ADE∽△ACB.
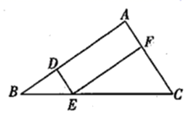
 13. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对.
13. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对. 14. 如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示 .
14. 如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示 . 15. 如图: 中, 是AB边上一点(与AB不重合),过点 作直线截 ,所截得的三角形与原 相似,满足这样条件的直线共有条.
15. 如图: 中, 是AB边上一点(与AB不重合),过点 作直线截 ,所截得的三角形与原 相似,满足这样条件的直线共有条. 16. 如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是(写出一个即可)
16. 如图,在△ABC中,点E,F分别在AB,AC上,若△AEF∽△ABC,则需要增加的一个条件是(写出一个即可)
三、解答题
-
17. 作出线段 的黄金分割点(不写作法,保留作图痕迹)
 18. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形.
18. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形. (1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .19. 如图,点E是正方形 的边 边上的黄金分割点,且 > , 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积,求 : 的值.
(1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .19. 如图,点E是正方形 的边 边上的黄金分割点,且 > , 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积,求 : 的值.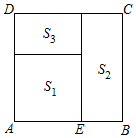 20. 如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB.
20. 如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB. 21. 如图,已知 ,点E、F在线段BD上, , ,求证:
21. 如图,已知 ,点E、F在线段BD上, , ,求证: