2022-2023学年北师大版数学九年级上册4.2平行线分线段成比例同步练习

试卷更新日期：2022-08-07 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图 $△ A B C$ 中， $E 、 F$ 分别在边 $A B 、 A C$ 上， $E F / / B C ， A B = 3 ， A E = 2 ， E F = 4$ ，则 $B C =$ （）

A、6 B、12 C、18 D、24

查看试题解析
2. 如图， $l_{1} // l_{2} // l_{3}$ ，直线a，b与 $l_{1} ， l_{2} ， l_{3}$ 分别交于点A、B、C和点D、E、F，若AB∶BC＝2∶3，EF＝6，则DE的长是（）

A、8 B、9 C、4 D、10

查看试题解析
3. 如图， $A D ∥ B E ∥ C F$ ，直线 $l_{1} ， l_{2}$ 与这三条平行线分别交于点A、B、C和点D、E、F，若 $A B = 9 ， B C = 6 ， E F = 4$ ，则DE的长度是（）

A、 $\frac{8}{3}$ B、 $\frac{27}{2}$ C、6 D、10

查看试题解析
4. 在 $△ A B C$ 中，点E、D、F分别在边AB、BC、AC上，联结DE、DF，如果 $D E ∥ A C$ ， $D F ∥ A B$ ， $A E ： E B = 3 ： 2$ ，那么 $A F ： F C$ 的值是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 已知线段a，b，c，求作线段x，使 $x = \frac{a c}{b}$ ，下列作法中正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，点D、E分别在△ABC的边AB、BC上，下列条件中一定能判定DE $∥$ AC的是（）

A、 $\frac{A D}{D B} = \frac{B E}{C E}$ B、 $\frac{B D}{A D} = \frac{B E}{E C}$ C、 $\frac{A D}{A B} = \frac{C E}{B E}$ D、 $\frac{B D}{B A} = \frac{D E}{A C}$

查看试题解析
7. 如图，直线a//b//c，直线 $l_{1}$ 、 $l_{2}$ 与这三条平行线分别交于点A、B、C和点D、E、F．若 $A B ： B C = 1 ： 2$ ， $D E = 3$ ，则EF的长为（）

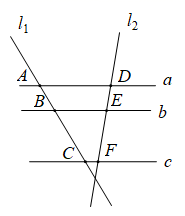A、1.5 B、6 C、9 D、12

查看试题解析
8. 如图，点E，D，F在△ABC的三边上，四边形AEDF是菱形，若 $\frac{F C}{A F} = \frac{3}{5}$ ，则 $\frac{B E}{A F}$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{5}{8}$ C、 $\frac{5}{3}$ D、 $\frac{8}{5}$

查看试题解析
9. 如图， $A B$ ， $C D$ 相交于点 $E$ ，且 $A C / / E F / / D B$ ，点 $C$ ， $F$ ， $B$ 在同一条直线上．已知 $A C = p$ ， $E F = r$ ， $D B = q$ ，则 $p$ ， $q$ ， $r$ 之间满足的数量关系式是（）

A、 $\frac{1}{r} + \frac{1}{q} = \frac{1}{p}$ B、 $\frac{1}{p} + \frac{1}{r} = \frac{2}{q}$ C、 $\frac{1}{p} + \frac{1}{q} = \frac{1}{r}$ D、 $\frac{1}{q} + \frac{1}{r} = \frac{2}{p}$

查看试题解析
10. 已知，如图 $l_{1} / / l_{2} / / l_{3}$ 下面等式： $(1) \frac{A B}{A C} = \frac{A D}{C F}$ ； $(2) \frac{B C}{C A} = \frac{E F}{F D}$ ； $(3) \frac{A B}{D E} = \frac{A C}{D F}$ ； $(4) \frac{A B}{D E} = \frac{A D}{B E}$ $(5) \frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}$ ，能成立的等式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，在ΔABC中，BC＝20，点B₁ ， B₂ ， B₃ ， B₄和点C₁ ， C₂ ， C₃ ， C₄分别是AB，AC的5等分点，则B₁C₁＋B₂C₂＋B₃C₃＋B₄C₄的值为。

查看试题解析
12. 如图，已知l₁∥l₂∥l₃ ，直线AB分别交l₁、l₂、l₃于A、M、B，直线CD分别交l₁、l₂、l₃于C、N、D，AM＝4，MB＝6，CD＝9，那么ND＝．

查看试题解析
13. 我们知道：四个角对应相等，四条边对应成比例的两个四边形是相似四边形．如图，已知梯形ABCD中，AD $∥$ BC，AD＝1，BC＝2，E、F分别是边AB、CD上的点，且EF $∥$ BC，如果四边AEFD与四边形EBCF相似，那么 $\frac{A E}{E B}$ 的值是．

查看试题解析
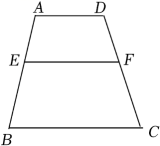14. 将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为.

查看试题解析
15. 在 $△ A B C$ 中， $D E ∥ B C$ ， $D E$ 分别交 $A B$ 、 $A C$ 于点 $D$ 、 $E$ ，已知 $A B = 6$ ， $A D = 2$ ， $E C = 3$ ，则 $A E =$ .

查看试题解析
16. 如图，在△ABC中，点D是AB边上的一点，且AD＝3BD，连接C并取CD的中点E，连接BE，若∠ACD＝∠BED＝45°，且CD＝6 $\sqrt{2}$ ，则AB的长为．

查看试题解析

三、解答题（共8题，共52分）

17.

(1)、如图1，在平行四边形ABCD中，点E₁ ， E₂是AB三等分点，点F₁ ， F₂是CD三等分点，E₁F₁ ， E₂F₂分别交AC于点G₁ ， G₂ ，求证：AG₁＝G₁G₂＝G₂C.

(2)、如图2，由64个边长为1的小正方形组成的一个网格图，线段MN的两个端点在格点上，请用一把无刻度的尺子，画出线段MN三等分点P，Q.(保留作图痕迹)

查看试题解析
18. 如图，在 $△ A B C$ 中，点D为 $B C$ 边上一点，连接 $A D$ ，点H为 $A D$ 中点，延长 $B H$ 交 $A C$ 边于点E，求证： $\frac{A E}{C E} = \frac{B D}{B C}$ ．

查看试题解析
19. 如图，在△ABC中，EF∥CD ，DE∥BC ．求证：AF：FD=AD：DB ．

查看试题解析
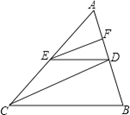20. 已知：如图，在△ABC中，∠ACB的平分线CD交AB于D，过B作BE∥CD交AC的延长线于点E.

(1)、求证：BC = CE；

(2)、求证： $\frac{A D}{B D} = \frac{A C}{B C}$

查看试题解析
21. 如图，已知AB∥CD，AD、BC 交于点E.

(1)、写出所有比值等于 $\frac{A E}{B E}$ 的两条线段之比.

(2)、若AE=3，DE=6，BC=12，求CE的长.

查看试题解析
22. 如图：已知在平行四边形ABCD中，E是AD上一点，CE与BD相交于点O，CE与BA的延长线相交于点G，已知DE＝2AE，CE＝10．

(1)、 $\frac{A E}{B C} =$ ， $\frac{O D}{O B}$ ＝．

(2)、求GE的长；

(3)、求CO的长．

查看试题解析
23. 如图，在等腰直角三角形ABC中，∠BAC=90°，已知A(1，0)，B(0，3)，M为边BC的中点。

(1)、求点C的坐标；

(2)、设点M的坐标为(a，b)，求 $\frac{b}{a}$ 的值；

(3)、探究：在x轴上是否存在点P，使以O、P、M为顶点的三角形与△OBM相似？若存在，请求出点P的坐标：若不存在，请简述理由。

查看试题解析
24. △ABC中，点D是BC边上的一点，点F在AD上，连接BF并延长交AC于点E；

(1)、如图1，若D为BC的中点， $\frac{A E}{E C} = \frac{1}{2}$ ，求证：AF＝FD；

(2)、尺规作图：在图2中，请利用圆规和无刻度的直尺在AC上找一点E，使得 $\frac{A E}{E C} = \frac{1}{2}$ ；

(3)、若F为AD的中点，设 $\frac{B D}{B C} = m ， \frac{A E}{A C} = n$ ，请求出m、n之间的等量关系.

查看试题解析

2022-2023学年北师大版数学九年级上册4.2平行线分线段成比例 同步练习

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共52分）

2022-2023学年北师大版数学九年级上册4.2平行线分线段成比例同步练习