2022-2023学年北师大版数学九年级上册3.2用频率估计概率同步练习

试卷更新日期：2022-08-07 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 某鱼塘里养了若干条草鱼、100条鲤鱼和50条罗非鱼，通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右．可估计该鱼塘中鱼的总数量为（）．

A、300 B、200 C、150 D、250

查看试题解析
2. 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在0.15和0.45，则布袋中白色球的个数可能是（）

A、24 B、18 C、16 D、6

查看试题解析
3. 育种小组对某品种小麦发芽情况进行测试，在测试条件相同的情况下，得到如下数据：
抽查小麦粒数
100
300
800
1000
2000
3000
发芽粒数
96
287
770
958
1923
a
则a的值最有可能是（）

A、2700 B、2780 C、2880 D、2940

查看试题解析
4. 下表记录了一名球员在罚球线上投篮的结果：
投篮次数
50
100
150
200
250
400
500
800
投中次数
28
63
87
122
148
242
301
480
投中频率
0.560
0.630
0.580
0.610
0.592
0.605
0.602
0.600
根据频率的稳定性，估计这名球员投篮一次投中的概率约是（）

A、0.560 B、0.580 C、0.600 D、0.620

查看试题解析
5. 做随机抛掷一枚纪念币的试验，得到的结果如下表所示：
抛掷次数m
500
1000
1500
2000
2500
3000
4000
5000
“正面向上”的次数n
265
512
793
1034
1306
1558
2083
2598
“正面向上”的频率 $\frac{n}{m}$
0.530
0.512
0.529
0.517
0.522
0.519
0.521
0.520
下面有3个推断：
①当抛掷次数是1000时，“正面向上”的频率是0.512，所以“正面向上”的概率是0.512；
②随着试验次数的增加，“正面向上”的频率总在0.520附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.520；
③若再次做随机抛掷该纪念币的实验，则当抛掷次数为3000时，出现“正面向上”的次数不一定是1558次．其中所有合理推断的序号是（）

A、② B、①③ C、②③ D、①②③

查看试题解析
6. 投掷一枚质地均匀的硬币m次，正面向上n次，下列表达正确的是（）

A、 $\frac{n}{m}$ 的值一定是 $\frac{1}{2}$ B、 $\frac{n}{m}$ 的值一定不是 $\frac{1}{2}$ C、m越大， $\frac{n}{m}$ 的值越接近 $\frac{1}{2}$ D、随着m的增加， $\frac{n}{m}$ 的值会在 $\frac{1}{2}$ 附近摆动，呈现出一定的稳定性

查看试题解析
7. 甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（　　）

A、掷一枚正六面体的骰子，出现1点的概率 B、一个袋子中有2个白球和1个红球，从中任取一个球，则取到红球的概率 C、抛一枚硬币，出现正面的概率 D、任意写一个整数，它能被2整除的概率

查看试题解析

8. “十一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”区域的次数m	68	108	140	355	560	690
落在“铅笔”区域的频率 $\frac{m}{n}$	0.68	0.72	0.70	0.71	0.70	0.69

下列说法错误的是（）

A、转动转盘20次，一定有6次获得“文具盒”铅笔文具盒 B、转动转盘一次，获得“铅笔”的概率大约是0.70 C、再转动转盘100次，指针落在“铅笔”区域的次数不一定是68次 D、如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次

查看试题解析

9. 下列说法错误的是（）

A、必然事件发生的概率为1 B、平均数和方差都不易受极端值的影响 C、抽样调查抽取的样本是否具有代表性，直接关系对总体估计的准确程度 D、可以通过大量重复试验，用一个随机事件发生的频率去估计它的概率

查看试题解析
10. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为5m，宽为4m的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计试验结果），他将若干次有效试验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（）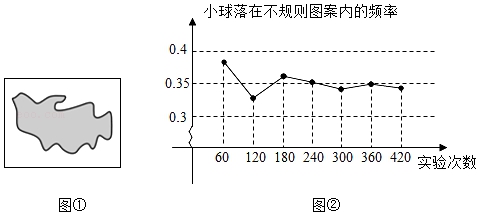

A、6m² B、7m² C、8m² D、9m²

查看试题解析

二、填空题（每题3分，共18分）

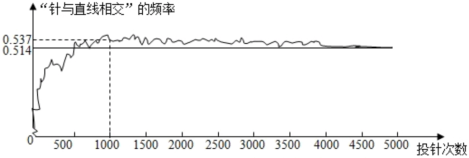
11. 一个不透明的盒子中装有8个白球和若干个红球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验1000次，其中有199次摸到红球，由此估计盒子中的红球大约有个．

查看试题解析
12. 小红利用计算机模拟“投针试验”：在一个平面上画一组间距为 $d = 0.73$ cm的平行线，将一根长度为 $l = 0.59$ cm的针任意投掷在这个平面上，针可能与某一直线相交，也可能与任一直线都不相交．下图显示了小红某次实验的结果，那么可以估计出针与直线相交的概率是（结果保留小数点后两位）．

查看试题解析
13. 某水果公司以2.2元/千克的成本价购进10000kg苹果，公司想知道苹果的损坏率，从所有苹果中随机抽取若干进行统计，部分结果如表：
抽取的苹果总质量
100
200
300
400
500
1000
损坏苹果质量
10.60
19.42
30.63
39.24
49.54
101.10
苹果损坏的频率
0.106
0.097
0.102
0.098
0.099
0.101
①估计这批苹果损坏的概率为（精确到0.1）；
②据此，若公司希望这批苹果能获得利润23000元，则销售时（去掉损坏的苹果）售价应定为元/千克．

查看试题解析
14. 一个不透明的袋子里装有黑白两种颜色的球共60个，这些球除颜色外都相同.小贤从袋子中随机摸一个球，记下颜色后放回，不断重复，并绘制了如图所示的统计图，则这个袋中黑球的个数最有可能是.

查看试题解析
15. 如图，创新广场上铺设了一种新颖的石子图案，它由五个过同一点且半径不同的圆组成，其中阴影部分铺黑色石子，其余部分铺白色石子．小鹏在规定地点随意向图案内投掷小球，每球都能落在图案内，经过多次试验，发现落在一、三、五环（阴影）内的概率分别是0.04，0.2，0.36，如果最大圆的半径是1米，那么黑色石子区域的总面积约为平方米（精确到0.01平方米）．

查看试题解析
16. 某商场举办抽奖活动，每张奖券获奖的可能性相同，以10000奖券为一个开奖单位，设特等奖10个，一等奖100个，二等奖500个，则1张奖券中奖的概率是．

查看试题解析

三、解答题（共8题，共52分）

17. 4件同型号的产品中，有1件不合格品和3件合格品.在这4件产品中加入 $x$ 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，由此可以推算出 $x$ 的值大约是多少？

查看试题解析
18. 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一球记下颜色，再把它放回盒子，不断重复上述过程实验n次，下表是小明“摸到白球”的频数、频率统计表.
摸球实验次数n
10
100
150
200
500
…
摸到白球的频数m
2
22
31
39
101
…
摸到白球的频率p
0.200
0.220
0.207
0.195
0.202
…

(1)、观察上表，可以推测，摸一次摸到白球的概率为.

(2)、请你估计盒子里白球个数.

(3)、若往盒子中同时放入x个白球和y个黑球，从盒子中随机取出一个白球的概率是0.25，求y与x之间的函数关系式.

查看试题解析
19. 只有1和它本身两个因数且大于1的正整数叫做素数．我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”．如20＝3＋17

(1)、从7、11、13、17这4个素数中随机抽取一个，则抽到的数是7的概率是．

(2)、从7、11、13、17这4个素数中随机抽取1个数，再从余下的3个数中随机抽取1个数，用画树状图或列表的方法，求抽到的两个素数之和等于24的概率．

查看试题解析

20. 有一个圆形转盘，分黑色、白色两个区域.

(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：

实验次数n(次)	10	100	2000	5000	10000	50000	100000
白色区域次数m(次)	3	34	680	1600	3405	16500	33000
落在白色区域频率 $\frac{m}{n}$	0.3	0.34	0.34	0.32	0.34	0.33	0.33

请你利用上述实验，估计转动该转盘指针落在白色区域的概率为

(2)、若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为240°，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.

查看试题解析

21. 对一批衬衣进行抽检，统计合格衬衣的件数，得到合格衬衣的频率表如下：

抽取件数	50	100	150	200	500	800	1000
合格频数	42	88	141	176	445	724	901
合格频率	0.84	a	0.94	0.88	0.89	0.91	b

(1)、计算表中a，b的值并估计任抽一件衬衣是合格品的概率.

(2)、估计出售2000件衬衣，其中次品大约有几件.

查看试题解析

22. 某地响应国家号召，将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其它垃圾四类，并分别设置了相应的垃圾箱.为调查该地居民生活垃圾的正确分类投放情况，现随机抽取了该地四类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：

	“厨余垃圾”箱	“可回收物”箱	“有害垃圾”箱	“其它垃圾”箱
厨余垃圾	400	100	40	60
可回收物	30	140	10	20
有害垃圾	5	20	60	15
其他垃圾	25	15	20	40

(1)、估算该地“有害垃圾”被正确投放在“有害垃圾箱”的概率.

(2)、已知该地一个月有5600吨生活垃圾，问投放错误的有害垃圾大约有几吨？

查看试题解析

23. 一只不透明的袋子中装有

4

个质地、大小均相同的小球，这些小球分别标有数字

3 、 4 、 5 、 x

，甲、乙两人每次同时从袋中各随机摸出

1

个球，并计算摸出的这

2

个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表

摸球总次数	10	20	30	60	90	120	180	240	330	450
“和为 $8$ ”出现的频数	2	10	13	24	30	37	58	82	110	150
“和为 $8$ ”出现的频率	0.20	0.50	0.43	0.40	0.363	0.31	0.32	0.34	0.33	0.33

解答下列问题：

(1)、如果实验继续进行下去，根据上表数据，出现“和为8”的频率将稳定在它的概率附近．估计出现“和为8”的概率是；

(2)、如果摸出的这两个小球上数字之和为

9

的概率是

\frac{1}{3}

，那么

x

的值可以取

7

吗？请用列表法或画树状图法说明理由；如果

x

的值不可以取

7

，请写出一个符合要求的

x

值．

查看试题解析

24. 苗木种植不仅绿了家园，助力脱贫攻坚，也成为乡村增收致富的“绿色银行”．小王承包了一片荒山，他想把这片荒山改造成一个苹果园，现在有一种苹果树苗，它的成活率如下表所示：
移植棵数（n）
成活数（m）
成活率（ $\frac{m}{n}$ ）
移植棵数（n）
成活数（m）
成活率（ $\frac{m}{n}$ ）
50
47
0.940
1500
1335
0.890
270
235
0.870
3500
3203
0.915
400
369
0.923
7000
6335
$x$
750
662
0.883
14000
12628
0.902
根据以上信息，回答下列问题：

(1)、当移植的棵数是7000时，表格记录成活数是，那么成活率x是

(2)、随着移植棵数的增加，树苗成活的频率总在0.900附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是

(3)、若小王移植10000棵这种树苗，则可能成活；

(4)、若小王移植20000棵这种树苗，则一定成活18000棵．此结论符合题意吗？说明理由．

查看试题解析

抽查小麦粒数	100	300	800	1000	2000	3000
发芽粒数	96	287	770	958	1923	a

投篮次数	50	100	150	200	250	400	500	800
投中次数	28	63	87	122	148	242	301	480
投中频率	0.560	0.630	0.580	0.610	0.592	0.605	0.602	0.600

抛掷次数m	500	1000	1500	2000	2500	3000	4000	5000
“正面向上”的次数n	265	512	793	1034	1306	1558	2083	2598
“正面向上”的频率 $\frac{n}{m}$	0.530	0.512	0.529	0.517	0.522	0.519	0.521	0.520

抽取的苹果总质量	100	200	300	400	500	1000
损坏苹果质量	10.60	19.42	30.63	39.24	49.54	101.10
苹果损坏的频率	0.106	0.097	0.102	0.098	0.099	0.101

摸球实验次数n	10	100	150	200	500	…
摸到白球的频数m	2	22	31	39	101	…
摸到白球的频率p	0.200	0.220	0.207	0.195	0.202	…

移植棵数（n）	成活数（m）	成活率（ $\frac{m}{n}$ ）	移植棵数（n）	成活数（m）	成活率（ $\frac{m}{n}$ ）
50	47	0.940	1500	1335	0.890
270	235	0.870	3500	3203	0.915
400	369	0.923	7000	6335	$x$
750	662	0.883	14000	12628	0.902

2022-2023学年北师大版数学九年级上册3.2用频率估计概率 同步练习

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共52分）

2022-2023学年北师大版数学九年级上册3.2用频率估计概率同步练习