2022-2023学年北师大版数学九年级上册3.1用树状图或表格求概率 同步练习
试卷更新日期：2022-08-07 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 连续两次掷一枚质地均匀的硬币，两次都是正面朝上的概率是 （ ）A、 B、 C、 D、2. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动，甲被选中的概率为（ ）A、 B、 C、 D、3. 在一个不透明纸箱中放有除了数字不同外，其它完全相同的2张卡片，分别标有数字1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之和为奇数的概率为（ ）A、 B、 C、 D、4. 小明和小华玩“石头、剪子、布”的游戏．若随机出手一次，则小华获胜的概率是（ ）A、 B、 C、 D、5. 笼子里关着一只小松鼠（如图）.笼子主人决定把小松鼠放归大自然，将笼子所有的门都打开，松鼠要先过第一道门（A或B），再过第二道门（C，D或E）才能出去，则松鼠走出笼子的路线是“先经过A门、再经过D门”的概率为（ ）
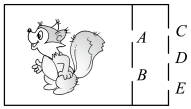A、 B、 C、 D、6. 有4张背面相同的卡片，正面分别印有平行四边形、矩形、菱形、正方形，现将4张卡片正面朝下一字摆开，从中随机抽取两张，抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为（ ）A、1 B、 C、 D、7. 为了深化落实“双减”工作，促进中小学生健康成长，教育部门加大了实地督查的力度，对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查，计划从“五项管理”中随机抽取两项进行问卷调查，则抽到“作业”和“手机”的概率为（ ）A、 B、 C、 D、8. 经过某十字路口的汽车，可能直行，也可能向左转或向右转．如果这三种可能性大小相同，甲、乙两辆汽车经过这个十字路口时，一辆车向左转，一辆车向右转的概率是（ ）A、 B、 C、 D、9. 一个不透明的袋子中装有四个小球，它们除了分别标有的数字1，2，3，6不同外，其他完全相同，任意从袋子中摸出一球后不放回，再任意摸出一球，则两次摸出的球所标数字之积为6的概率是（ ）A、 B、 C、 D、10. 如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以构成一个矩形，从这些矩形中任选一个，则所选矩形含点P的概率是（ ）
A、 B、 C、 D、二、填空题（每题3分，共18分）
-
11. 某中学举办庆祝中国共产党建党100周年党史知识竞赛．某班有5名学生报名，其中2男3女，计划从这5名学生中随机抽选两名学生参加知识竞赛，所选两名学生中恰好1男1女的概率为 ．12. 有4张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．将这4张纸牌背面朝上洗匀后先由小明从中任意摸出一张，放回洗匀后再由小敏从中任意摸出一张，则“小明所摸纸牌是中心对称图形，小敏所摸纸牌是轴对称图形”的概率为 ．
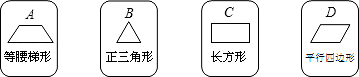13. 从﹣1，π， ， 1，6中随机取两个数，取到的两个数都是无理数的概率是 ．14. 时隔十三年，奥运圣火再次在北京点燃．北京将首次举办冬奥会，成为国际上唯一举办过夏季和冬季奥运会的“双奥之城”．墩墩和融融积极参加雪上项目的训练，现有三辆车按照1，2，3编号，两人可以任选坐一辆车去训练，则两人同坐2号车的概率是 ．15. 有4张正面分别标有数字﹣3、1、2、3的卡片，它们除数字不同外其余完全相同，现将它们背面朝上，从中随机抽出2张卡片，则抽出的两张卡片上的数字之积为奇数的概率是.16. 如图，是两个可以自由转动的转盘，转盘各被等分为三个扇形，并分别标有2、3、4和6、7、8这6个数字，如果同时转动这两个转盘各一次（指针落在等分线上重转），转盘停止后，则指针指向的数字之和为奇数的概率为 ．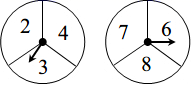
三、解答题（共8题，共52分）
-
17. 从-2，-1，2三个数中任取两个不同的数，作为点的坐标，用列表法或画树状图求该点在第三象限的概率．18. 我国新冠灭活疫苗主要来自三家生物制品公司，分别是A：科兴中维、B：北京所、C：武汉所．灭活疫苗一般需要接种2针，假如一人两次接种的疫苗的生产公司随机，请你用列表或树状图的方法求出一个人两次接种的疫苗刚好是同一家公司生产的概率．19. 现有A、B两个不透明的袋子，A袋中的两个小球分别标记数字1，2；B袋中的三个小球分别标记数字3，4，5．这五个小球除标记的数字外，其余完全相同．分别将A、B两个袋子中的小球摇匀，然后小明从A、B袋中各随机摸出一个小球，请利用画树状图或列表的方法，求小明摸出的这两个小球标记的数字之和为5的概率．20. 现有三位“抗疫”英雄（依次标记为A，B，C）．为了让同学们了解他们的英雄事迹，张老师设计了如下活动：取三张完全相同的卡片，分别在正面写上A，B，C三个标号，然后背面朝上放置，搅匀后请一位同学从中随机抽取一张，记下标号后放回，要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.(1)、求班长在这三种卡片中随机抽到标号为C的概率；(2)、用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.21. 在一个不透明的口袋里装有分别标注 1、2 的两个小球 (小球除数字外， 其余都相同)， 另有背面完全一样、正面分别写有 3、4、5 的三张卡片， 现从口袋中任意摸出一个小球， 再从这三张背面朝上的卡片中任意摸出一张， 则(1)、共有多少种结果? （请用列表或者画树状图的方法表示说明）(2)、小方和小圆选择下列两个规则中的一个做游戏：
①若两次摸出的数字， 和为奇数， 则小方赢， 否则小圆赢；
②若两次摸出的数字， 积为奇数， 则小方赢， 否则小圆赢。
小方想要在游戏中获胜机会更大些， 他应选择哪一条规则， 请说明理由.
22. 2021年教育部出台了关于中小学生作业、睡眠、手机、读物、体质五个方面的管理，简称“五项管理”，这是推进立德树人，促进学生全面发展的重大举措.某班为培养学生的阅读习惯，利用课外时间开展以“走近名著”为主题的读书活动，有6名学生喜欢四大名著，其中2人（记为 ， ）喜欢《西游记），2人（记为 ， ）喜欢《红楼梦》，1人（记为C）喜欢《水浒传》，1人（记为D）喜欢《三国演义》.(1)、如果从这6名学生中随机抽取1人担任读书活动宣传员，求抽到的学生恰好喜欢《西游记》的概率.(2)、如果从这6名学生中随机抽取2人担任读书活动宣传员，求抽到的学生恰好1人喜欢《西游记》1人喜欢《红楼梦》的概率.23. 为了更好地解决养老问题，某服务中心引入优质社会资源为甲，乙两个社区共30名老人提供居家养老服务，收集得到这30名老人的年龄（单位：岁）如下：甲社区
68
69
73
75
76
78
80
82
83
84
85
85
90
92
95
乙社区
67
69
72
74
75
78
80
81
85
85
88
89
91
96
98
根据以上信息解答下列问题：
(1)、求甲社区老人年龄的中位数和众数；(2)、现从两个社区年龄在70岁以下的4名老人中随机抽取2名了解居家养老服务情况，求这2名老人恰好来自同一个社区的概率．24. 为了解班级学生参加课后服务的学习效果，何老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：A：很好；B：较好；C：一般；D：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：
(1)、此次调查的总人数为；(2)、扇形统计图中“不达标”对应的圆心角度数是°；(3)、请将条形统计图补充完整；(4)、为了共同进步，何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.