湖南省长沙市长沙县2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，四边形 $A B C D$ 中， $\vec{A B} = \vec{D C}$ ，则相等的向量是（）

A、 $\vec{A D}$ 与 $\vec{C B}$ B、 $\vec{O B}$ 与 $\vec{O D}$ C、 $\vec{A C}$ 与 $\vec{B D}$ D、 $\vec{A O}$ 与 $\vec{O C}$

查看试题解析
2. 设复数z满足 $z = 2 - i$ （其中i为虚数单位），则 $| z | =$ （）

A、 $\sqrt{5}$ B、 $\sqrt{2}$ C、5 D、 $\sqrt{3}$

查看试题解析
3. 圆柱内有一个球 $O$ ，该球与圆柱的上、下底面及母线均相切，已知圆柱的体积为 $16 π$ ，则球 $O$ 的体积为（）

A、 $\frac{32 π}{3}$ B、 $\frac{64 π}{3}$ C、16π D、12π

查看试题解析
4. 为了丰富高一学生的课外生活，某校要组建数学、计算机、航空模型、绘画4个兴趣小组，小明要随机选报其中的2个，则该试验中样本点的个数为（）

A、3 B、5 C、6 D、9

查看试题解析
5. “治国之道，富民为始.”共同富裕是社会主义的本质要求，是中国式现代化的重要特征，是人民群众的共同期盼.共同富裕是全体人民通过辛勤劳动和相互帮助最终达到丰衣足食的生活水平，是消除两极分化和贫穷基础上的普遍富裕．请你运用数学学习中所学的统计知识加以分析，下列关于个人收入的统计量中，最能体现共同富裕要求的是（）

A、平均数小，方差大 B、平均数小，方差小 C、平均数大，方差大 D、平均数大，方差小

查看试题解析
6. 设l，m，n均为直线，其中m，n在平面 $α$ 内，“ $l ⊥ α$ ”是“ $l ⊥ m$ 且 $l ⊥ n$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 如图所示，在平行四边形 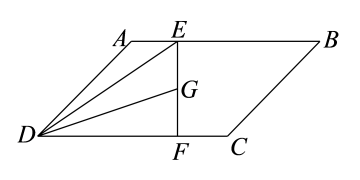$A B C D$ 中， $A E = \frac{1}{4} A B ， C F = \frac{1}{4} C D$ ， $G$ 为 $E F$ 的中点，则 $\vec{D G} =$ （）

A、 $\frac{1}{2} \vec{A D} - \frac{1}{2} \vec{A B}$ B、 $\frac{1}{2} \vec{A B} - \frac{1}{2} \vec{A D}$ C、 $\frac{3}{4} \vec{A D} - \frac{1}{2} \vec{A B}$ D、 $\frac{3}{4} \vec{A B} - \frac{1}{2} \vec{A D}$

查看试题解析
8. 人类通常有O，A，B，AB四种血型，某一血型的人可以给哪些血型的人输血，是有严格规定的．设X代表O，A，B，AB中某种血型，箭头左边表示供血者，右边表示受血者，则输血规则如下：①X→X；②O→X；③X→AB．已知我国O，A，B，AB四种血型的人数所占比例分别为41%，28%，24%，7%，在临床上，按照上述规则，若受血者为A型血，则一位供血者能为这位受血者正确输血的概率为（）

A、0.31 B、0.48 C、0.65 D、0.69

查看试题解析

二、多选题

9. 下列命题错误的是（）

A、 $a ∥ b$ ， $b \subset α \Rightarrow a ∥ α$ B、 $a ∥ α$ ， $b \subset α \Rightarrow a ∥ b$ C、 $a ∥ α$ ， $a ∥ b \Rightarrow b ∥ α$ D、 $a ⊄ α$ ， $a ∥ b$ ， $b \subset α \Rightarrow a ∥ α$

查看试题解析
10. 在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，且 $a = 2$ 、 $b = 3$ 、 $c = 4$ ，下面说法错误的是（）

A、 $s i n A ： s i n B ： s i n C = 2 ： 3 ： 4$ B、 $△ A B C$ 是锐角三角形 C、 $△ A B C$ 的最大内角是最小内角的 $2$ 倍 D、 $△ A B C$ 内切圆半径为 $\frac{1}{2}$

查看试题解析
11. 下列命题中是真命题的有（）

A、有A，B，C三种个体按 $3 ︰ 1 ︰ 2$ 的比例分层抽样调查，如果抽取的A个体数为9，则样本容量为30 B、一组数据1，2，3，3，4，5的平均数、众数、中位数相同 C、若甲组数据的方差为5，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是甲 D、某一组样本数据为125，120，122，105，130，114，116，95，120，134，则样本数据落在区间 $[114.5 ， 124.5]$ 内的频率为0.4

查看试题解析
12. 如图所示是正方体的平面展开图，那么在正方体中（）

A、 $A C ⊥ E F$ B、EF和BC所成的角是60° C、直线AC和平面ABE所成的角是30° D、如果平面 $A B C ∩$ 平面 $C E F = l$ ，那么直线 $E F ∥$ 直线 $l$ .

查看试题解析

三、填空题

13. 我国2021年9月至2022年3月的居民消费指数（上年同月＝100）分别为100.7，101.5，102.3，101.5，100.9，100.9，101.5，则这组数据的第20百分位数是．

查看试题解析
14. 从甲、乙、丙三人中任选两名代表，甲被选中的概率为.

查看试题解析
15. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，则点B到直线 $A C_{1}$ 的距离为．

查看试题解析
16. 已知 $A D$ 是 $△ A B C$ 的中线，若 $∠ A = 12 0^{∘}$ ， $\vec{A B} \cdot \vec{A C} = - 2$ ，则 $| \vec{A D} |$ 的最小值是．

查看试题解析

四、解答题

17. 已知复数 $z_{1} = 3 + 4 i$ ， $z_{2} = - 2 i$ ， i为虚数单位．

(1)、若 $z = \frac{z_{1}}{z_{2}}$ ，求z的共轭复数；

(2)、若复数 $z_{1} + a z_{2}$ 在复平面上对应的点在第一象限，求实数a的取值范围．

查看试题解析
18. 从1~30这30个整数中随机选择一个数，设事件M表示选到的数能被2整除，事件N表示选到的数能被3整除．求下列事件的概率：

(1)、这个数既能被2整除也能被3整除；

(2)、这个数能被2整除或能被3整除；

(3)、这个数既不能被2整除也不能被3整除．

查看试题解析
19. 已知向量 $\vec{a} = (6 ， 1)$ ， $\vec{b} = (- 2 ， 3)$ ， $\vec{c} = (2 ， 2)$ ， $\vec{d} = (- 3 ， k)$ ．

(1)、求 $\vec{a} + 2 \vec{b} - \vec{c}$ ；

(2)、若 $(\vec{a} + 2 \vec{c}) / / (\vec{c} + k \vec{b})$ ，求实数 $k$ 的值．

(3)、若 $\vec{a}$ 与 $\vec{d}$ 的夹角是钝角，求实数 $k$ 的取值范围．

查看试题解析
20. 在锐角△ABC中，A，B，C的对边分别为a，b，c，且 $\sqrt{3} a = 2 c s i n A$ ．

(1)、求角C的大小；

(2)、若 $c = \sqrt{7}$ ，且 $a b = 6$ ，求△ABC的周长．

查看试题解析
21. 2019年下半年以来，各地区陆续出台了“垃圾分类”的相关管理条例，实行“垃圾分类”能最大限度地减少垃圾处置量，实现垃圾资源利用，改善垃圾资源环境，某部门在某小区年龄处于 $[20 ， 45]$ 岁的人中随机地抽取 $x$ 人，进行了“垃圾分类”相关知识掌握和实施情况的调查，并把达到“垃圾分类”标准的人称为“环保族”，得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
组数
分组
“环保族”人数
占本组的频率
第一组
$[20 ， 25)$
45
0.75
第二组
$[25 ， 30)$
25
$y$
第三组
$[30 ， 35)$
20
0.5
第四组
$[35 ， 40)$
$z$
0.2
第五组
$[40 ， 45)$
3
0.1

(1)、求 $x$ 、 $y$ 、 $z$ 的值；

(2)、根据频率分布直方图，估计这 $x$ 人年龄的平均值（同一组数据用该区间的中点值代替，结果按四舍五入保留整数）；

(3)、从年龄段在 $[25 ， 35]$ 的“环保族”中采取分层抽样的方法抽取9人进行专访，并在这9人中选取2人作为记录员，求选取的2名记录员中至少有一人年龄在 $[30 ， 35]$ 中的概率.

查看试题解析
22. 如图，四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面ABCD为平行四边形，侧面 $A D D_{1} A_{1}$ 为矩形， $A B = 2 A D = 2$ ， $∠ D_{1} D B = 60 °$ ， $B D = A A_{1} = \sqrt{3}$ .

(1)、证明：平面 $A B C D ⊥$ 平面 $B D D_{1} B_{1}$ ；

(2)、求三棱锥 $D_{1} - B C B_{1}$ 的体积.

查看试题解析

组数	分组	“环保族”人数	占本组的频率
第一组	$[20 ， 25)$	45	0.75
第二组	$[25 ， 30)$	25	$y$
第三组	$[30 ， 35)$	20	0.5
第四组	$[35 ， 40)$	$z$	0.2
第五组	$[40 ， 45)$	3	0.1