湖南省岳阳市临湘市2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 设z= $\frac{1}{1 + i}$ +i，则|z|=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、2

查看试题解析
2. 2021年湖南省新高考实行“3+1+2”模式，即语文、数学、外语必选，物理、历史二选一，政治、地理、化学、生物四选二，共有12种选课模式．某同学已选了物理，记事件A=“他选择政治和地理”，事件B=“他选择化学和地理”，则事件A与事件B（）

A、是互斥事件，不是对立事件 B、是对立事件 C、既不是对立事件，也不是互斥事件 D、无法判断

查看试题解析
3. 已知两条不同直线 $l$ ， $m$ ，两个不同平面 $α$ ， $β$ ，则下列命题正确的是（）

A、若 $α / / β$ ， $l \subset α$ ， $m \subset β$ ，则 $l / / m$ B、若 $α / / β$ ， $m / / α$ ， $l ⊥ β$ ，则 $l ⊥ m$ C、若 $α ⊥ β$ ， $l ⊥ α$ ， $m ⊥ β$ ，则 $l / / m$ D、若 $α ⊥ β$ ， $l / / α$ ， $m / / β$ ，则 $l ⊥ m$

查看试题解析
4. 设 $x \in R$ ，则“ $x^{2} - 5 x < 0$ ”是“ $| x - 1 | < 1$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 已知 $a = l o g_{2} \frac{1}{2}$ ， $b = {(\frac{1}{2})}^{- 2}$ ， $c = 2^{\frac{1}{2}}$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $b < c < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
6. 如图，测量河对岸的塔高 $A B$ 时，可以选与塔底 $B$ 在同一水平面内的两个观测点 $C$ ， $D$ ，测得 $∠ B C D = 15 °$ ， $∠ C B D = 30 °$ ， $C D = 10 \sqrt{2} m$ ，并在 $C$ 处测得塔顶 $A$ 的仰角为45°，则塔高 $A B =$ （）

A、 $30 \sqrt{2} m$ B、 $20 \sqrt{3} m$ C、 $30 m$ D、 $20 m$

查看试题解析
7. 函数 $f (x) = x + c o s x$ 的零点所在的区间为（）

A、 $(- 1 ， - \frac{1}{2})$ B、 $(- \frac{1}{2} ， 0)$ C、 $(0 ， \frac{1}{2})$ D、 $(\frac{1}{2} ， 1)$

查看试题解析
8. 已知四边形 $A B C D$ 中， $A C ⊥ B D$ ， $A B = B C = \frac{B D}{2} = 2$ ， $A C = C D = 2 \sqrt{3}$ ，点 $E$ 在四边形 $A B C D$ 上运动，则 $\vec{E B} \cdot \vec{E D}$ 的最小值是（）

A、3 B、-1 C、-3 D、-4

查看试题解析

二、多选题

9. 为了解学生的身体状况，某校随机抽取了100名学生测量体重，经统计，这些学生的体重数据（单位：千克）全部介于45至70之间，将数据整理得到如图所示的频率分布直方图，则（）

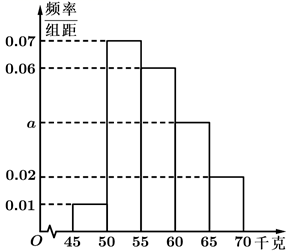A、频率分布直方图中 $a$ 的值为0.04 B、这100名学生中体重不低于60千克的人数为20 C、这100名学生体重的众数约为52.5 D、据此可以估计该校学生体重的75%分位数约为61.25

查看试题解析
10. 将函数 $f (x) = s i n (2 x - φ) (0 < φ < \frac{π}{2})$ 的图象上所有的点向左平行移动 $\frac{π}{3}$ 个单位长度，得到偶函数 $h (x)$ 的图象，则下列结论中正确的有（）

A、 $h (x)$ 的图象关于点 $(- \frac{π}{4} ， 0)$ 对称 B、 $h (x)$ 的图象关于 $x = \frac{π}{2}$ 对称 C、 $h (x)$ 在 $[\frac{π}{12} ， \frac{2 π}{3}]$ 上的值域为 $[- \frac{1}{2} ， \frac{\sqrt{3}}{2}]$ D、 $h (x)$ 在 $[\frac{π}{6} ， \frac{π}{2}]$ 上单调递减

查看试题解析
11. 下列说法正确的是（）

A、若函数 $f (x)$ 在 $(- 1 ， 1)$ 存在零点，则 $f (- 1) \cdot f (1) < 0$ 一定成立 B、“ $\forall x \in R$ ， $x^{2} - 2 x - 3 \neq 0$ ”的否定是“ $\exists x_{0} \in R$ ， $x_{0}^{2} - 2 x_{0} - 3 = 0$ ” C、设M为平行四边形ABCD的对角线的交点，O为平面内任意一点，则 $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 2 \vec{O M}$ D、若 $2 \vec{O A} + \vec{O B} + 3 \vec{O C} = \vec{0}$ ，O为 $△ A B C$ 所在平面一点， $S_{△ B O C}$ 和 $S_{△ A B C}$ 分别表示 $△ B O C$ 和 $△ A B C$ 的面积，则 $S_{△ B O C} ： S_{△ A B C} = 1 ： 3$

查看试题解析
12. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $P$ 在线段 $B_{1} C$ 上运动，则（）

A、直线 $B D_{1} ⊥$ 平面 $A_{1} C_{1} D$ B、二面角 $B_{1} - C D - B$ 的大小为 $\frac{π}{2}$ C、三棱锥 $P - A_{1} C_{1} D$ 的体积为定值 D、异面直线 $A P$ 与 $A_{1} D$ 所成角的取值范围是 $[\frac{π}{4} ， \frac{π}{2}]$

查看试题解析

三、填空题

13. 已知向量 ${b_{n}}$ ， $\vec{n} = (c o s \frac{x}{4} ， c o s^{2} \frac{x}{4})$ ，若 $\vec{m} ⊥ \vec{n}$ ，则 $c o s (x - \frac{π}{3}) =$ ．

查看试题解析
14. 关于 $x$ 的方程 $x^{2} + (2 a - i) x - a i + 1 = 0$ 有实根，则实数 $a$ 的值为．

查看试题解析
15. 为了了解一家公司生产的白糖的质量情况，现从这家公司生产的白糖中随机抽取了10袋白糖，称出各袋白糖的质量（单位：克）如下：
495 500 503 508 498 500 493 500 503 500

则质量落在区间 $[\bar{x} - s ， \bar{x} + s]$ （ $\bar{x}$ 表示质量的平均值， $s$ 为标准差）内的白糖有袋.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} | l n x | ， 0 < x \leq 2 \\ f (4 - x) ， 2 < x < 4 \end{array}$ ，若当方程 $f (x) = m$ 有四个不等实根 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ ， ( $x_{1}$ ＜ $x_{2}$ ＜ $x_{3}$ ＜ $x_{4}$ ) 时，不等式 $k x_{3} \cdot x_{4} + x_{1}^{2} + x_{2}^{2} \geq k + 11$ 恒成立，则x₁·x₂= ，实数 $k$ 的最小值为．

查看试题解析

四、解答题

17. 已知 $\vec{m} = （ s i n x ， - \sqrt{3} ）$ ， $\vec{n} = (c o s x ， c o s^{2} x ）$ 函数 $f (x) = \vec{m} \cdot \vec{n}$ ．

(1)、求 $f (x)$ 的最小正周期和最大值；

(2)、求 $f (x)$ 在 $[\frac{π}{6} ， \frac{2 π}{3}]$ 上的单调区间．

查看试题解析
18. 从① $(a - c) (a + c) = b (a - b)$ ，② $\sqrt{3} a \cos C = c \sin A$ ，③ $\cos^{2} (\frac{π}{2} + C) + \cos C = \frac{5}{4}$ 三个条件中任选一个补充在下面问题中，并解答：
已知 $△ A B C$ 三个内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知_________.

(1)、求角 $C$ 的大小；

(2)、若 $△ A B C$ 为锐角三角形， $b = 2$ ，求a的取值范围.

查看试题解析
19. 在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $D$ ， $E$ 分别是 $A A_{1}$ ， $B_{1} C_{1}$ 的中点．
（Ⅰ）求证： $A_{1} E / /$ 平面 $C_{1} B D$ ；
（Ⅱ）若 $D C_{1} ⊥ B D$ ， $A C = B C = 1$ ， $A A_{1} = 2$ ．
（ⅰ）求二面角 $B - D C_{1} - C$ 的正切值；
（ⅱ）求直线 $A_{1} E$ 到平面 $C_{1} B D$ 的距离．

查看试题解析

20. 为打造精品赛事，某市举办“南粤古驿道定向大赛”，该赛事体现了“体育+文化+旅游”全方位融合发展.本次大赛分少年组、成年组、专业组三个小组，现由工作人员统计各个组别的参赛人数以及选手们比赛时的速度，得到如下统计表和频率分布直方图：

组数	速度（千米/小时）	参赛人数（单位：人）
少年组	$[6 ， 8)$	300
成年组	$[8 ， 10)$	600
专业组	$[10 ， 12]$	$b$

(1)、求a ， b的值；

(2)、估计本次大赛所有选手的平均速度（同一组数据用该组数据的中间值作代表，最终计算结果精确到0.01）；

(3)、通过分层抽样从成年组和专业组中抽取6人，再从这6人中随机抽取2人接受采访，求接受采访的2人都来自“成年组”的概率.

查看试题解析

21. 十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划，2020年某企业计划引进新能源汽车生产设备看，通过市场分析，全年需投入固定成本 $3000$ 万元，每生产 $x$ （百辆）需另投入成本 $y$ （万元），且 $y = {\begin{array}{l} 10 x^{2} + 100 x ， 0 < x < 40 \\ 501 x + \frac{10000}{x} - 4500 ， x \geq 40 \end{array}$ .由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完.

(1)、求出2020年的利润 $S$ （万元）关于年产量 $x$ （百辆）的函数关系式；（利润=销售额—成本）

(2)、当2020年产量为多少百辆时，企业所获利润最大？并求出最大利润.

查看试题解析
22. 已知函数 $f (x) = \frac{4^{x} + b}{2^{x}}$ 为奇函数．

(1)、求实数 $b$ 的值；

(2)、若对任意的 $x \in [0 ， 1]$ ，有 $f (2 x^{2} - k x - k) + \frac{3}{2} < 0$ 恒成立，求实数 $k$ 的取值范围；

(3)、设 $g (x) = \log_{m} [4^{x} + 4^{- x} - m f (x)]$ （ $m > 0$ ，且 $m \neq 1$ ），问是否存在实数 $m$ ，使函数 $g (x)$ 在 $[1 ， \log_{2} 3]$ 上的最大值为 $0$ ？若存在，求出 $m$ 的值，若不存在，请说明理由．

查看试题解析