湖南省五市十校教研教改共同体2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $M = {x | x = 2 n ， n \in Z}$ ， $N = {x | x = 2 n + 1 ， n \in Z}$ ， $P = {x | x = 4 n ， n \in Z}$ ，则（）

A、 $M ⊊ P$ B、 $P ⊊ M$ C、 $N ∩ P \neq \emptyset$ D、 $M ∩ N \neq \emptyset$

查看试题解析
2. 已知某射击运动员每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击3次，至少击中2次的概率，先由计算器输出0到9之间取整数值的随机数，指定0.1表示没有击中目标，2，3，4，5，6，7，8，9表示击中目标.因为射击3次，故以每3个随机数为一组，代表射击3次的结果，经随机模拟产生了以下20组随机数：
572   029   714   985   034   437   863   964   141   469
037   623   261   804   601   366   959   742   671   428
据此估计，该射击运动员射击3次至少击中2次的概率约为（   ）

A、0.8 B、0.85 C、0.9 D、0.95

查看试题解析
3. 设 $0 < θ < \frac{π}{2}$ ， $a = c o s^{2} θ$ ， $b = 2^{c o s θ}$ ， $c = l o g_{2} c o s θ$ ，则 $a$ ， $b$ ， $c$ 的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $a < c < b$ D、 $c < a < b$

查看试题解析
4. 已知函数 $f (x) = l o g_{a} (x - b)$ （ $a > 0$ 且 $a \neq 1$ ， $a$ ， $b$ 为常数）的图象如图，则下列结论正确的是（）

A、 $a > 0$ ， $b < - 1$ B、 $a > 0$ ， $- 1 < b < 0$ C、 $0 < a < 1$ ， $b < - 1$ D、 $0 < a < 1$ ， $- 1 < b < 0$

查看试题解析
5. 若 $s i n (\frac{π}{6} - α) = \frac{1}{2}$ ，则 $c o s (\frac{π}{3} - 2 α) =$ （）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
6. 已知 $a ， b ， c \in R$ ，在下列条件中，使得 $a < b$ 成立的一个充分而不必要条件是（）

A、 $a^{3} < b^{3}$ B、 $a c^{2} < b c^{2}$ C、 $\frac{1}{a} > \frac{1}{b}$ D、 $a^{2} < b^{2}$

查看试题解析
7. 函数 $f (x) = s i n (\frac{π}{2} x) - l o g_{0.2} x (x > 0)$ 的零点个数为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 设 $A$ ， $B$ ， $C$ ， $D$ 是平面内四个不同的点，且 $(\vec{A B} + \vec{C D}) \cdot (| C D | \vec{A B} + | A B | \vec{C D}) = 0$ ，则向量 $\vec{A B}$ 与 $\vec{C D}$ （）

A、同向平行 B、反向平行 C、互相垂直 D、既不平行也不垂直

查看试题解析

二、多选题

9. 对于任意两个向量 $\vec{a} ， \vec{b}$ ，下列命题正确的是（）

A、 $| \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} |$ B、 $| \vec{a} - \vec{b} | \leq | \vec{a} | - | \vec{b} |$ C、 $| \vec{a} \cdot \vec{b} | \leq | \vec{a} | \cdot | \vec{b} |$ D、若 $| \vec{a} | > | \vec{b} |$ ，则 $\vec{a} > \vec{b}$

查看试题解析
10. 下列命题中正确的是（）

A、若复数 $z$ 满足 $\bar{z} \in R$ ，则 $z \in R$ B、若复数 $z$ 满足 $z \cdot \bar{z} \in R$ ，则 $z \in R$ C、若复数 $z$ 满足 $z^{2} \geq 0$ ，则 $z \in R$ D、若复数 $z$ 满足 $\frac{1}{z} \in R$ ，则 $z \in R$

查看试题解析
11. 已知直线 $x = \frac{π}{6}$ 是函数 $f (x) = s i n (2 x + φ) (0 < φ < π)$ 的一条对称轴，则（）

A、点 $(\frac{π}{6} ， 0)$ 是函数 $f (x)$ 的一个对称中心 B、函数 $f (x)$ 在 $[\frac{π}{6} ， \frac{2 π}{3}]$ 上单调递减 C、函数 $y = f (x)$ 的图像可由 $y = s i n 2 x$ 的图像向左平移 $\frac{π}{6}$ 个单位长度得到 D、函数 $y = f (x)$ 与 $g (x) = s i n (2 x - \frac{π}{6})$ 的图像关于直线 $x = \frac{π}{4}$ 对称

查看试题解析
12. 在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A A_{1} = 1$ ，点 $P$ 满足 $\vec{A P} = \vec{A B} + λ \vec{B C} + μ \vec{B B_{1}}$ ，其中 $λ \in [0 ， 1]$ ， $μ \in [0 ， 1]$ ，则下列说法正确的是（）

A、当 $λ + μ = 1$ 时，则存在点 $P$ ，使得 $C P ∥ B A_{1}$ B、当 $λ + μ = 1$ 时，则存在点 $P$ ，使得 $B$ ， $P$ ， $C_{1}$ 三点共线 C、当 $λ = \frac{1}{2}$ 时，则存在点 $P$ ，使得 $A_{1}$ ， $B_{1}$ ， $C$ ， $P$ 四点共面 D、当 $μ = \frac{1}{2}$ 时，则存在点 $P$ ，使得 $A_{1} B ⊥ A P$

查看试题解析

三、填空题

13. 设z＝ $\frac{1}{1 + i}$ ＋i(i为虚数单位)，则|z|＝.

查看试题解析
14. 若 $| \vec{O A} | = 1$ ， $| \vec{O B} | = 4$ ， $\vec{O A} \cdot \vec{O B} = 2$ ，则以 $O A$ ， $O B$ 为邻边的平行四边形的面积是.

查看试题解析
15. 已知圆锥的底面半径为 $\sqrt{3}$ ，其侧面展开图为一个半圆，则该圆锥的内切球（球与圆锥的底面和侧面均相切）的表面积为.

查看试题解析
16. 拿破仑定理是法国著名军事家拿破仑·波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆圆心恰为另一个等边三角形（此等边三角形称为拿破仑三角形）的顶点”.在 $△ A B C$ 中，已知 $∠ A C B = 30 °$ ，且 $A B = \sqrt{3} - 1$ ，现以 $B C$ ， $A C$ ， $A B$ 为边向外作三个等边三角形，其外接圆圆心依次记为 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ，则 $△ A^{'} B^{'} C^{'}$ 的面积最大值为.

查看试题解析

四、解答题

17. 已知函数 $f (x) = s i n (x + \frac{π}{4}) c o s (x + \frac{3 π}{4}) + \frac{1}{2}$

(1)、讨论函数 $y = f (x)$ 的周期性和奇偶性；

(2)、若 $f (α) = \frac{1}{4}$ ， $α \in (0 ， π)$ ，求 $α$ 的值.

查看试题解析
18. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ 分别是线段 $A_{1} B_{1}$ ， $B C$ 的中点.

(1)、证明： $E F ∥$ 平面 $A A_{1} C_{1} C$ ；

(2)、若 $A B = B C = 2$ ，直线 $E F$ 与 $B B_{1}$ 所成角的余弦值是 $\frac{\sqrt{3}}{3}$ ，求四面体 $B E F B_{1}$ 的体积.

查看试题解析
19. 读书可以增长知识，开拓视野，修身怡情.树人中学为了解本校学生课外阅读情况，按性别进行分层，用分层随机抽样的方法从全校学生中抽出一个容量为100的样本，其中男生40名，女生60名.经调查统计，分别得到40名男生一周课外阅读时间（单位：小时）的频数分布表和60名女生一周课外阅读时间（单位：小时）的频率分布直方图.
男生一周阅读时间频数分布表
小时
频数
$[0 ， 2)$
9
$[2 ， 4)$
25
$[4 ， 6)$
3
$[6 ， 8)$
3

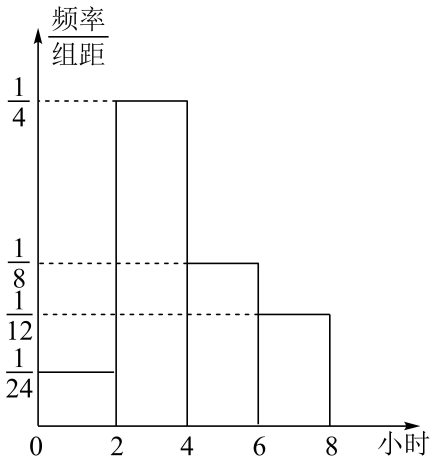(1)、由以上频率分布直方图估计该校女生一周阅读时间的众数和75%分位数；

(2)、由以上频数分布表和频率分布直方图估计总样本的平均数 $\bar{z}$ ；

(3)、从一周课外阅读时间为 $[4 ， 6)$ 的样本学生中按比例分配抽取6人，再从这6人中任意抽取2人，求恰好抽到一男一女的概率.
（注：以各组的区间中点值代表该组的各个值）

查看试题解析
20. 如图，在三棱锥 $A - B C D$ 中， $A B$ ， $B C$ ， $C D$ 两两互相垂直， $M$ ， $N$ 分别是 $A D$ ， $B C$ 的中点.

(1)、证明： $M N ⊥ B C$ ；

(2)、设 $B C = 2$ ， $A D = 2 \sqrt{5}$ ， $M N$ 和平面 $B C D$ 所成角的大小为 $\frac{π}{6}$ ，求二面角 $A - C D - B$ 的大小.

查看试题解析
21. 目前，新冠还在散发，防疫任重道远，经济下行，就业压力大，为此，国家大力提倡大学生自主创业.小李大学毕业后在同一城市开了 $A$ ， $B$ 两家小店，每家店各有2名员工.五一期间，假设每名员工请假的概率都是 $\frac{1}{2}$ ，且是否请假互不影响.若某店的员工全部请假，而另一家店没有人请假，则调剂1人到该店以维持正常运转，否则该店就关门停业.

(1)、求有员工被调剂的概率；

(2)、求至少有一家店停业的概率.

查看试题解析
22. 已知 $△ A B C$ 的三个内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $\vec{A B} \cdot \vec{A C} + \vec{B A} \cdot \vec{B C} = 2 \vec{C A} \cdot \vec{C B}$

(1)、若 $\frac{c o s A}{b} = \frac{c o s B}{a}$ ，判断 $△ A B C$ 的形状并说明理由；

(2)、若 $△ A B C$ 是锐角三角形，求 $s i n C$ 的取值范围.

查看试题解析

男生一周阅读时间频数分布表
小时	频数
$[0 ， 2)$	9
$[2 ， 4)$	25
$[4 ， 6)$	3
$[6 ， 8)$	3