2022-2023学年苏科版数学八年级上册2.2.2轴对称的性质应用同步训练
试卷更新日期:2022-08-05 类型:同步测试
一、单选题
-
1. 如图,作 关于直线对称的图形 ,接着 沿着平行于直线 的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )
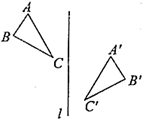 A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分2. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( )
A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分2. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( ) A、1个 B、2个 C、3个 D、4个3. 下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( )
A、1个 B、2个 C、3个 D、4个3. 下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则的度数为( )
4. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则的度数为( ) A、 B、 C、 D、5. 如图,已知D为边的中点,E在上,将沿着折叠,使A点落在上的F处.若 , 则等于( )
A、 B、 C、 D、5. 如图,已知D为边的中点,E在上,将沿着折叠,使A点落在上的F处.若 , 则等于( ) A、65 B、 C、 D、6. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )
A、65 B、 C、 D、6. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )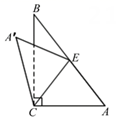 A、10° B、15° C、20° D、40°
A、10° B、15° C、20° D、40°二、填空题
-
7. 如图,在平面直角坐标系 中, 可以看作是 经过若干次的图形变化(轴对称、平移)得到的,写出一种由 得到 的过程: .
 8. 如图,点P是∠AOB内任意一点,∠AOB=30°点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则OP的长是.
8. 如图,点P是∠AOB内任意一点,∠AOB=30°点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则OP的长是. 9. 如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字的格子内.
9. 如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字的格子内.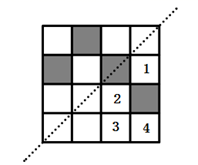 10. 如图, , 点和点分别在边和边上,连接 , 将沿折叠,点的对应点是 , 若 , 则 .
10. 如图, , 点和点分别在边和边上,连接 , 将沿折叠,点的对应点是 , 若 , 则 .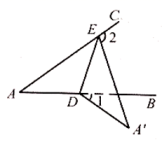 11. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=70°,则∠BDF的度数为 .
11. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=70°,则∠BDF的度数为 . 12. 如图,把的一角折叠,若 , 则的度数为 .
12. 如图,把的一角折叠,若 , 则的度数为 .
三、作图题
-
13. 如图,在平面直角坐标系中,已知点A(1,4),B(4,4),C(2,1).

(1)请在图中画出 ABC;
(2)将 ABC向左平移5个单位,再沿x轴翻折得到 A1B1C1 , 请在图中画出 A1B1C1;
(3)若 ABC 内有一点P(a,b),则点P经上述平移、翻折后得到的点P1的坐是 .14. 图1、图2、图3都是3×3的正方形网格,每个小正方形的顶点称为格点, 、 、 均为格点.在给定的网格中,按下列要求画图: (1)、在图1中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 、 为格点;(2)、在图2中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 、 为格点;(3)、在图3中,画一个 ,使 与 关于某条直线对称,且 、 、 为格点,符合条件的三角形共有个.
(1)、在图1中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 、 为格点;(2)、在图2中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 、 为格点;(3)、在图3中,画一个 ,使 与 关于某条直线对称,且 、 、 为格点,符合条件的三角形共有个.四、综合题
-
15.(1)、如图,已知四边形 ,请用直尺和圆规在边 上求作一点 ,使 (不写作法,保留作图痕迹)
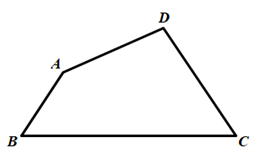 (2)、请根据(1)的作图过程,说明 的理由.16. 阅读理解
(2)、请根据(1)的作图过程,说明 的理由.16. 阅读理解如图①,△ABC 中,沿∠BAC 的平分线 AB1 折叠,剪掉重复部分;将余下部分沿∠B1A1C 的平分线 A1B2 折叠,剪掉重复部分;….;将余下部分沿∠BnAnC 的平分线 AnBn+1 折叠, 点 Bn 与点 C 重合.无论折叠多少次,只要最后一次恰好重合,∠BAC 是△ABC 的好角. 小丽展示了确定∠BAC 是△ABC 的好角的两种情形.情形一:如图②,沿等腰三角形ABC 顶角∠BAC 的平分线 AB1 折叠,点 B 与点 C 重合;情形二:如图③,沿∠BAC 的平分线 AB1 折叠,剪掉重复部分;将余下的部分沿∠B1A1C 的平分线 A1B2 折叠,此时点 B1 与点 C 重合.
 (1)、探究发现
(1)、探究发现
△ABC 中,∠B=2∠C,∠BAC 是不是△ABC 的好角?(填“是”或“不是”)(2)、猜想:若经过 n 次折叠后发现∠BAC 是△ABC 的好角,则∠B 与∠C(不妨设∠B > ∠C )之间的等量关系为;(3)、应用提升
小丽找到一个三角形,三个角分别为 15°、60°、105°,发现 60°和 105°的两个角都是此三角形的好角.请你完成,如果一个三角形的最小角是 12°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.