2022-2023学年苏科版数学八年级上册2.2.1轴对称的性质同步训练
试卷更新日期:2022-08-05 类型:同步测试
一、单选题
-
1. 下列结论中不正确的是( )A、两个关于某直线对称的图形一定全等 B、对称图形的对称点一定在对称轴的两侧 C、两个成轴对称的图形对应点的连线的垂直平分线是它们的对称轴 D、有斜边和一锐角相等的两个直角三角形全等2. 如图,△ABC与△DEF关于直线1对称,BE交l于点O , 则下列说法不一定正确的是( )
 A、AC=DF B、BO=EO C、AB=EF D、l是线段AD的垂直平分线3. 如图,作 关于直线对称的图形 ,接着 沿着平行于直线 的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )
A、AC=DF B、BO=EO C、AB=EF D、l是线段AD的垂直平分线3. 如图,作 关于直线对称的图形 ,接着 沿着平行于直线 的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )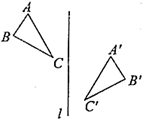 A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分4. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分4. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )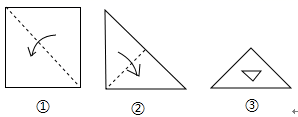 A、
A、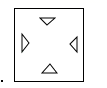 B、
B、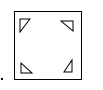 C、
C、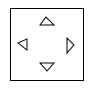 D、
D、 5. 剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
5. 剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( )
6. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是°.
 8. 如图,在四边形ABCD中,∠C=55°,∠B=∠D=90°,E,F分别是线段BC,DC上的动点,当 周长最小时,∠EAF的度数为.
8. 如图,在四边形ABCD中,∠C=55°,∠B=∠D=90°,E,F分别是线段BC,DC上的动点,当 周长最小时,∠EAF的度数为. 9. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为
9. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为 10. 下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有.(填序号)11. 已知两条互不平行的线段 和 关于直线L对称, 和 所在的直线交于点P,下面四个结论:① ;②点P在直线L上;③若A、 是对应点,则直线L垂直平分线段 ;④若B、 是对应点,则 ,其中正确的是(填序号).
10. 下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有.(填序号)11. 已知两条互不平行的线段 和 关于直线L对称, 和 所在的直线交于点P,下面四个结论:① ;②点P在直线L上;③若A、 是对应点,则直线L垂直平分线段 ;④若B、 是对应点,则 ,其中正确的是(填序号). 12. 如图,已知点 .规定“把点 先作关于 轴对称,再向左平移1个单位”为一次变换.经过第一次变换后,点 的坐标为;经过第二次变换后,点 的坐标为;那么连续经过2019次变换后,点 的坐标为 .
12. 如图,已知点 .规定“把点 先作关于 轴对称,再向左平移1个单位”为一次变换.经过第一次变换后,点 的坐标为;经过第二次变换后,点 的坐标为;那么连续经过2019次变换后,点 的坐标为 .
三、解答题
-
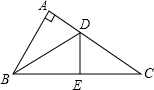
13. 如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.
 14. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
14. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58° (1)、求出BF的长度;(2)、求∠CAD的度数;15. 如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1 , P2是点P关于AB、AC的对称点,连结P1P2 , 分别交AB、AC于点D、E.
(1)、求出BF的长度;(2)、求∠CAD的度数;15. 如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1 , P2是点P关于AB、AC的对称点,连结P1P2 , 分别交AB、AC于点D、E.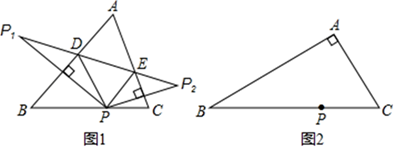 (1)、若∠A=52°,求∠DPE的度数;(2)、如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2 , (不写作法,保留作图痕迹),试判断点P1 , P2与点A是否在同一直线上,并说明理由.16. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
(1)、若∠A=52°,求∠DPE的度数;(2)、如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2 , (不写作法,保留作图痕迹),试判断点P1 , P2与点A是否在同一直线上,并说明理由.16. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.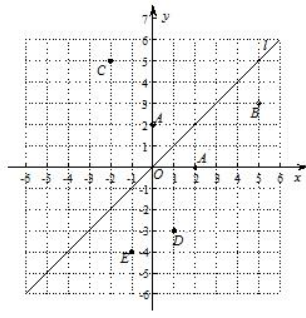 (1)、实验与探究:
(1)、实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;(2)、归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(不必证明);(3)、运用与发现:
已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小.