2022-2023学年苏科版数学八年级上册1.3.6探索三角形全等的条件HL同步训练
试卷更新日期:2022-08-05 类型:同步测试
一、单选题
-
1. 如图,已知BC=BD,那么添加下列一个条件后,仍无法判定△ABC≌△ABD的是( )
 A、AC=AD B、∠ABC=∠ABD C、∠C=∠D=90° D、∠CAB=∠DAB2. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( )
A、AC=AD B、∠ABC=∠ABD C、∠C=∠D=90° D、∠CAB=∠DAB2. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( ) A、8cm B、10cm C、12cm D、14cm3. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( )
A、8cm B、10cm C、12cm D、14cm3. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③4. 根据下列各图中所作的“边相等、角相等”标记,其中不能使该图中两个三角形全等的是( )A、
A、①②④ B、①②③④ C、②③④ D、①③4. 根据下列各图中所作的“边相等、角相等”标记,其中不能使该图中两个三角形全等的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在 和 中, , , ,过A作 ,垂足为F, 交 的延长线于点G,连接 .若四边形 的面积为12, ,则 的长是( )
5. 如图,在 和 中, , , ,过A作 ,垂足为F, 交 的延长线于点G,连接 .若四边形 的面积为12, ,则 的长是( ) A、2 B、2.5 C、3 D、
A、2 B、2.5 C、3 D、二、填空题
-
6. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是.
 7. 如图,OP平分∠AOB,PA OA,PB OB,垂足分别为点A、B.下列结论中,一定成立的是(填序号)
7. 如图,OP平分∠AOB,PA OA,PB OB,垂足分别为点A、B.下列结论中,一定成立的是(填序号)①PA=PB;②OA=OB;③OP垂直平分AB;④AB垂直平分OP
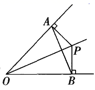 8. 如图, 中, 、 的角平分线 、 交于点P,延长 、 ,则下列结论中正确的有 . (将所有正确序号填在横线上)
8. 如图, 中, 、 的角平分线 、 交于点P,延长 、 ,则下列结论中正确的有 . (将所有正确序号填在横线上)① 平分 ;② ,③ ;④若 , ,则 .
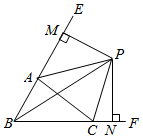 9. 如图, , 只需添加一个条件 , 就可以判定 .
9. 如图, , 只需添加一个条件 , 就可以判定 . 10. 如图,在 ABC中,AH是高,AE BC,AB=AE,在AB边上取点D,连接DE,DE=AC,若 ,BH=1,则BC=.
10. 如图,在 ABC中,AH是高,AE BC,AB=AE,在AB边上取点D,连接DE,DE=AC,若 ,BH=1,则BC=.
三、综合题
-
11. 如图所示,点B , E , C , F在同一条直线上,能否由 , 来证明AC∥DE?如果能,请给出证明;如果不能,请从下列四个条件中再选择一个合适的条件,使AC∥DE成立,并说明理由.供选择的四个条件:① ;② ;③AB∥DF;④ .
 12. 如图,已知AC平分∠BAD,CE⊥AB于E 点,∠ADC+∠B=180°.求证:
12. 如图,已知AC平分∠BAD,CE⊥AB于E 点,∠ADC+∠B=180°.求证: (1)、BC=CD;(2)、2AE=AB+AD.13. 如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,D为AH上一点,且BD=AC,直线BD与AC交于点E,连接EH.
(1)、BC=CD;(2)、2AE=AB+AD.13. 如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,D为AH上一点,且BD=AC,直线BD与AC交于点E,连接EH. (1)、求证:DH=CH;(2)、判断BE与AC的位置关系,并证明你的结论;(3)、求∠BEH的度数.14. 如图,在四边形ABCD中,和互补,CD=CB,于E.
(1)、求证:DH=CH;(2)、判断BE与AC的位置关系,并证明你的结论;(3)、求∠BEH的度数.14. 如图,在四边形ABCD中,和互补,CD=CB,于E. (1)、求证:AC平分;(2)、试猜想AB,AD,AE的数量关系并证明你的猜想.15. 如图,∠MON=90°,点A、B分别在射线OM、ON上,点C在∠MON内部.
(1)、求证:AC平分;(2)、试猜想AB,AD,AE的数量关系并证明你的猜想.15. 如图,∠MON=90°,点A、B分别在射线OM、ON上,点C在∠MON内部.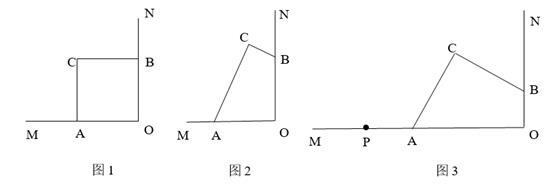 (1)、若OA=OB,
(1)、若OA=OB,①如图1,若CA⊥OM,CB⊥ON.求证:CA=CB.
②如图2,若∠ACB=90°.求证:OC平分∠ACB.
(2)、如图3,点A、B 分别在射线OM、ON上运动,点C随之运动,且∠ACB=90°,AC=BC.P为OM上一定点,当点C运动到何处时,PC的长度最短?请用尺规作图作出PC最短时C点的位置(保留作图痕迹,不要写作法),并请简要说明理由.