广东省深圳市南山区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 北京2022年冬奥会会徽(冬梦),是第24届冬季奥林匹克运动会使用的标志,主要由会徽图形、文字标志、奥林匹克五环标志组成,组成会徽的四个图案中是轴对称图形的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 长度为3,7,的三条线段构成三角形,则的值可能是( )A、3 B、4 C、8 D、123. 下列计算正确的是( )A、 B、 C、 D、4. 2022年3月深圳小区防疫封控期间,小明上完网课,去距家160米的检测点做核酸检测,他用了2分钟到达检测点,扫码检测共用了2分钟,由于不让在户外聚集,他及时回家用了2.5分钟.下列图象能符合题意表示小明离家的距离与时间关系的是( )A、
2. 长度为3,7,的三条线段构成三角形,则的值可能是( )A、3 B、4 C、8 D、123. 下列计算正确的是( )A、 B、 C、 D、4. 2022年3月深圳小区防疫封控期间,小明上完网课,去距家160米的检测点做核酸检测,他用了2分钟到达检测点,扫码检测共用了2分钟,由于不让在户外聚集,他及时回家用了2.5分钟.下列图象能符合题意表示小明离家的距离与时间关系的是( )A、 B、
B、 C、
C、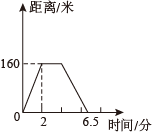 D、
D、 5. 已知一个等腰三角形有一个角为80°,则顶角是( )A、20° B、80° C、20°或80° D、不能确定6. 下列事件是必然事件的是( )A、抛一枚硬币,第一次抛正面朝上,第二次抛也是正面朝上 B、打开电视机中央一台,正在播放广告 C、袋中有4个黑球和2个白球,摸一次摸到黑球 D、任意画一个三角形,其内角和是7. 如图是一款手推车的平面示意图,其中AB∥CD , , ,则 的大小是( )
5. 已知一个等腰三角形有一个角为80°,则顶角是( )A、20° B、80° C、20°或80° D、不能确定6. 下列事件是必然事件的是( )A、抛一枚硬币,第一次抛正面朝上,第二次抛也是正面朝上 B、打开电视机中央一台,正在播放广告 C、袋中有4个黑球和2个白球,摸一次摸到黑球 D、任意画一个三角形,其内角和是7. 如图是一款手推车的平面示意图,其中AB∥CD , , ,则 的大小是( ) A、 B、 C、 D、8. 如图,在中, , . 若是的高,与角平分线相交于点 , 则的度数为( )
A、 B、 C、 D、8. 如图,在中, , . 若是的高,与角平分线相交于点 , 则的度数为( )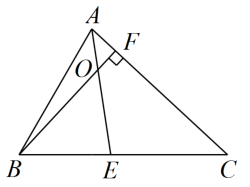 A、 B、 C、 D、9. 有足够多张如图所示的 类、 类正方形卡片和 类长方形卡片,如果要拼一个长为 、宽为 的大长方形,则需要 类卡片的张数为( )
A、 B、 C、 D、9. 有足够多张如图所示的 类、 类正方形卡片和 类长方形卡片,如果要拼一个长为 、宽为 的大长方形,则需要 类卡片的张数为( )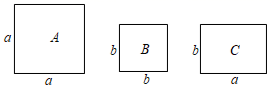 A、3 B、4 C、6 D、710. 如图,在中, , 是高,是中线,是角平分线,交于点 , 交于点 , 下面四个说法中,其中正确的是( )
A、3 B、4 C、6 D、710. 如图,在中, , 是高,是中线,是角平分线,交于点 , 交于点 , 下面四个说法中,其中正确的是( )①的面积等于的面积;②;③;④
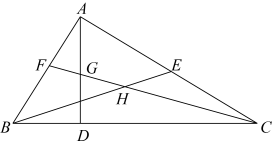 A、①②③④ B、①②③ C、②④ D、①③
A、①②③④ B、①②③ C、②④ D、①③二、填空题
-
11. 用科学记数法表示: .12. 如图,从以下给出的四个条件中选取一个:

① ;
② ;
③ ;
④ .
恰能判断 ∥ 的概率是 .
13. 如图, ABC的边AB的垂直平分线分别交BC、AB于点D、E,BC=5cm,AC=3cm,则 ADC的周长是cm. 14. 如图,点在上,点E在上, , 添加一个条件 , 使(填一个即可).
14. 如图,点在上,点E在上, , 添加一个条件 , 使(填一个即可). 15. 已知 ,则 .
15. 已知 ,则 .三、解答题
-
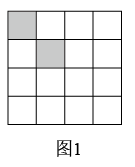
16. 计算:(1)、;(2)、;(3)、先化简,再求值: , 其中 , .17. 如图,在正方形网格中,阴影部分是由2个小正方形组成的图形,请你分别在下图方格内填涂2个小正方形,使这4个小正方形组成的图形满足:图1有且只有一条对称轴;图2有且只有两条对称轴;图3有且只有四条对称轴.

 18. 已知,如图所示,在中, .
18. 已知,如图所示,在中, . (1)、作的角平分线交于点;(要求:尺规作图,保留作图痕迹,不写作法.)(2)、若 , , 求的面积.19. 阅读下列推理过程,在括号中填写依据.
(1)、作的角平分线交于点;(要求:尺规作图,保留作图痕迹,不写作法.)(2)、若 , , 求的面积.19. 阅读下列推理过程,在括号中填写依据.已知:如图,点、分别在线段、上, , , 交于点 , 平分 .
求证:平分 .

证明:∵平分(已知).
∴(角平分线的定义).
∵(已知),
∴( ).
∴(等量代换).
∵(已知),
∴( ).
▲ (两直线平行,内错角相等).
∴( ).
∴平分(角平分线的定义).
20. 某公交车每天的支出费用为600元,每天乘车人数(人)与每天利润(利润=票款收入-支出费用)(元)的变化关系,如下表所示(每位乘客的乘车票价固定不变):(人)
…
200
250
300
350
400
…
(元)
…
-200
-100
0
100
200
…
根据表格中的数据,回答下列问题:
(1)、观察表中数据可知,当乘客量达到人以上时,该公交车才不会亏损;票价为(元/人);(2)、请写出公交车每天利润(元)与每天乘车人数(人)的关系式:;(3)、当一天乘客人数为多少人时,利润是1000元?

