广东省深圳市福田区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图案中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $- {(x^{2})}^{4} = - x^{6}$ B、 $x^{2} \cdot x^{3} = x^{5}$ C、 $x^{2} + x^{3} = x^{5}$ D、 $(x - y) (x + y) = x^{2} + y^{2}$

查看试题解析
3. 如图所示，工人师傅在砌门时，通常用木条 $B D$ 固定长方形门框 $A B C D$ ，使其不变形，这样做的数学根据是（）

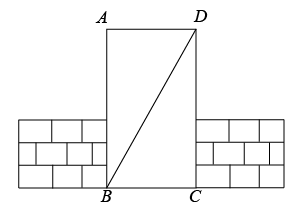A、两点确定一条直线 B、两点之间，线段最短 C、同角的余角相等 D、三角形具有稳定性

查看试题解析
4. 下列语句所描述的事件中，是不可能事件的是（）

A、黄河入海流 B、大漠孤烟直 C、手可摘星辰 D、红豆生南国

查看试题解析
5. 如图，已知 $∠ 1 = 68 °$ ，要使 $A B ∥ C D$ ，则需具备下列哪个条件（）

A、 $∠ 2 = 112 °$ B、 $∠ 2 = 132 °$ C、 $∠ 2 = 68 °$ D、 $∠ 3 = 112 °$

查看试题解析
6. 在测量一个小口圆形容器的壁厚（厚度均匀）时，小明用“ $X$ 型转动钳”按如图方法进行测量，其中 $O A = O D$ ， $O B = O C$ ，测得 $A B = 3$ 厘米， $E F = 4$ 厘米，圆形容器的壁厚是（）

A、2厘米 B、1.5厘米 C、1厘米 D、0.5厘米

查看试题解析
7. 一年365天，天安门广场的升旗仪式与太阳的节奏同步，唤醒一座城市的梦，唤醒一个国家的清晨．当升旗手匀速升旗时，旗子的高度 $h$ （米）与时间 $t$ （分）这两个变量之间的关系用图象可以表示为（）

A、 B、 C、 D、

查看试题解析
8. 下列说法错误的是（）

A、两直线平行，同旁内角互补 B、三角形一边上的中线正好把这个三角形分成两个面积相等的三角形 C、一个等腰三角形的两边长分别是2和4，则周长是8或10 D、角平分线上的任意一点到角两边的距离相等

查看试题解析
9. 如图，已知 $A B = A C ， A B = 5 ， B C = 3$ ，以 $A B$ 两点为圆心，大于 $\frac{1}{2} A B$ 的长为半径画圆，两弧相交于点 $M ， N$ ，连接 $M N$ 与 $A C$ 相较于点 $D$ ，则 $Δ B D C$ 的周长为（）

A、8 B、10 C、11 D、13

查看试题解析
10. 如图，正方形 $A B C D$ 与正方形 $A E F G$ 的边长分别为 $x$ ， $y$ ．若 $x y = 10$ ， $B E = \frac{3}{2}$ ，则图中阴影部分的面积为（）

A、5 B、 $\frac{39}{8}$ C、 $\frac{25}{4}$ D、 $\frac{41}{8}$

查看试题解析

二、填空题

11. 某种新冠病毒的直径为 $0.0000076 c m$ ，将数字0.0000076用科学记数法表示为 $7.6 \times 1 0^{n}$ ，则n= ．

查看试题解析
12. 已知 $x - y = 2$ ，则 $2^{x} \div 2^{y} =$ ．

查看试题解析
13. 如图，将一块含有 $30 °$ 角的直角三角板的两个顶点放在直尺的对边上．如果 $∠ 1 = 20 °$ ，那么 $∠ 2 =$ °．

查看试题解析
14. 某商场将一商品在保持销售价100元/件不变的前提下，规定凡购买超过5件者，所购商品全部打8折出售．若顾客购买 $x (x > 5)$ 件，应付 $y$ 元，则 $y$ 与 $x$ 间的关系式是 $y =$ ．

查看试题解析
15. 如图所示，将长方形纸片 $A B C D$ 折叠，使点 $D$ 与点 $B$ 重合，点 $C$ 落在点 $C^{'}$ 处，折痕为 $E F$ ，若 $∠ A B E = 20 °$ ，那么 $∠ E F C$ 的度数为．

查看试题解析

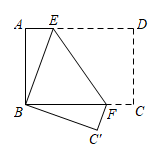
三、解答题

16. 计算：

(1)、 $(- 2022)^{0} + {(- \frac{1}{2})}^{- 2} + | - 3 |$

(2)、 ${(x y^{2})}^{2} \cdot (- 6 x^{3} y) \div (3 x^{4} y^{4})$

(3)、 $(x + 5) (x - 3)$

查看试题解析
17. 先化简，再求值： $[(x + 3 y)^{2} + 9 (x - y) (x + y)] \div (2 x)$ ，其中 $x = 1$ ， $y = - 2$ ．

查看试题解析
18. 概率与统计在我们日常生活中应用非常广泛，请同学们直接填出下列事件中所要求的结果：

(1)、我们平时娱乐的一副标准扑克去掉大小王后剩下的四种花色（红桃、方块、梅花、黑桃）共有52张，如果从中任抽一张得到红桃的概率为；

(2)、盒子里有红黑两种颜色的5个相同的球，如果随机抽取1个球记下颜色，然后放回，再重复这个试验，通过大量重复试验后发现，抽到红球的频率稳定在0.8左右，则盒中红球有个；

(3)、形如 $a^{2} \pm 2 a b + b^{2}$ 的式子称为完全平方式．若有一多项式为 $a^{2} + k a + 9$ ，其中 $k$ 的值可以从4张分别写有－3，－6，6，9的卡片中随机抽取，那么正好让这个多项式为完全平方式的概率为；

(4)、如图是由全等的小正方形组成的图案，假设可以随意在图中取点，那么这个点取在阴影部分的概率是．

查看试题解析
19. 如图，在长方形 $A B C D$ 中， $A D ∥ B C ， A B ∥ C D$ ， $M N$ 垂直平分 $A C$ 分别交 $A D$ ， $B C$ 于 $M$ ， $N$ ，求证： $C M = C N$ ．（请你将下面的推理过程中的横线空白处补充完整．）
解：∵ $A D ∥ B C$ （     ）
∴ $∠ D A C = ∠ A C B$ （     ）
∵ $M N$ 垂直平分 $A C$ （已知）
∴ $A O = C O$ （线段垂直平分线的定义）
在 $△ A M O$ 和 $△ C N O$ 中，
${\begin{array}{l} ∠ M A O = ∠ N C O \\ A O = C O \\ ∠ A O M = ∠ C O N (__) \end{array}$ ，
∴ $△ A O M ≌ △ C O N$ （     ）
∴ $A M = C N$ （     ）
又∵ $M N$ 垂直平分 $A C$ （已知）
∴      ▲ （线段垂直平分线上的点到线段两端的距离相等）
∴ $C M = C N$ （     ）．

查看试题解析
20. 如图，小胖用10块高度都是 $4 c m$ 的相同长方体积木，垒了两堵与地面垂直的木墙，木墙之间刚好可以把吴老师的一个大等腰直角三角板 $A B C$ 放进去（ $∠ A C B = 90 °$ ， $A C = B C$ ），点 $C$ 在 $D E$ 上，点 $A$ 和 $B$ 分别与木墙的顶端重合．

(1)、求证： $△ A D C ≌ △ C E B$ ．

(2)、吴老师看到这个模型很感兴趣，问小胖能否求出这个大等腰直角三角板 $A B C$ 的面积呢？小胖百思不得其解，请你来帮他解决．

查看试题解析
21. 一艘货船在甲、乙两港之间承接往返运输任务．某日货船从甲港顺流出发，途经丙港并不做停留，抵达乙港停留一段时间后逆流返航（始终保持同一航线）．货船在行驶过程中保持自身船速（即船在静水中的速度）不变，已知水流速度为8千米/时，如图记录了当日这艘货船出发后与乙港的距离 $y$ （千米）随时间 $t$ （小时）的变化的图象．图象上的点 $A$ 表示货船当日顺流航行到达丙港．（顺水速度＝静水速度＋水流速度；逆水速度＝静水速度－水流速度）

(1)、根据图象回答下列问题：甲乙两港之间的距离为千米；货船在乙港停留的时间为小时；

(2)、 $m =$ ， $n =$ ；

(3)、当 $t$ 为何值时这艘货船在往返途中距甲港80千米？

查看试题解析
22. 在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $C E$ 平分 $∠ A C B$ ， $B D$ 和 $C E$ 交于点 $O$ ，其中令 $∠ B A C = x$ ， $∠ B O C = y$ ．

(1)、【计算求值】如图1，①如果 $x = 50 °$ ，则 $y =$ ；②如果 $y = 130 °$ ，则 $x =$ ．

(2)、【猜想证明】如图2请你根据（1）中【计算求值】的心得猜想写出 $y$ 与 $x$ 的关系式为 $y =$ ▲ ，并请你说明你的猜想的正确性．

(3)、【解决问题】如图3，某校园内有一个如图2所示的三角形的小花园，花园中有两条小路， $B D$ 和 $C E$ 为三角形的角平分线，交点为点 $O$ ，在 $O$ 处建有一个自动浇水器，需要在 $B C$ 边取一处接水口 $F$ ，经过测量得知 $∠ B A C = 120 °$ ， $O D \cdot O E = 12000$ 米 $^{2}$ ， $B C - B E - C D = 170$ 米，请你求出水管 $O F$ 至少要多长？（结果取整数）

查看试题解析