广东省汕头市龙湖区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 $\frac{1}{3}$ ， 0， $\sqrt[3]{- 1}$ ， 3.1415926， $\sqrt{16}$ ， 4.21， $3 - π$ 中，有理数的个数为（）

A、3 B、4 C、5 D、6

查看试题解析
2. 如图所示的图案是一些汽车的车标，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 下列调查中，不适合用普查的是（）

A、了解全班同学每周体育锻炼的时长 B、“新冠”肺炎疫情期间检测地铁乘客的体温 C、某学校招艺术特长生，对报名学生进行面试 D、了解全国中学生每天写作业的时长

查看试题解析
4. 如图，点E在AC的延长线上，下列条件中能判断 $A B ∥ C D$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ 1 = ∠ 2$ C、 $∠ D = ∠ D C E$ D、 $∠ D + ∠ A C D = 180 °$

查看试题解析
5. 不等式3x+4≥1的解集是（）

A、 B、 C、 D、

查看试题解析
6. 用加减消元法解二元一次方程组 ${\begin{matrix} x + 3 y = 4 ① \\ 2 x - y = 1 ② \end{matrix}$ 时，下列方法中无法消元的是（）

A、①×2﹣② B、②×（﹣3）﹣① C、①×（﹣2）+② D、①﹣②×3

查看试题解析
7. 一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠A＝60°，则∠DBC的度数为（）

A、45° B、25° C、15° D、20°

查看试题解析
8. 已知a、b分别是 $3 + \sqrt{5}$ 的整数部分和小数部分，则b－2a的值是（）

A、 $\sqrt{5} - 12$ B、 $12 - \sqrt{5}$ C、 $\sqrt{5} - 8$ D、 $8 - \sqrt{5}$

查看试题解析
9. 如图，在一次“寻宝”游戏中，寻宝人找到了如图所示的两个标志点A（3，1），B（2，2），则“宝藏”点C的位置是（）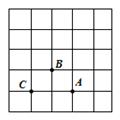

A、（1，0） B、（1，2） C、（2，1） D、（1，1）

查看试题解析
10. 如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC.其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. “a 与2的和是非负数”用不等式表示为

查看试题解析
12. $\sqrt{81}$ 的平方根是．

查看试题解析
13. 已知点A在x轴上方，y轴左侧，到x轴的距离是3，到y轴的距离是4，那么点A的坐标是．

查看试题解析
14. 若 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程x﹣2y=0的解，则3a﹣6b﹣3= ．

查看试题解析
15. 如图，直线l₁∥l₂ ，并被直线l₃所截，若∠1＝125°，则∠2＝°．

查看试题解析
16. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为。

查看试题解析
17. 对于实数s、t，我们用符号 max{s，t}表示s、t两数中较大的数，如max{3，1}=3．若max{ x²－10，3x²}=6，则 x= ．

查看试题解析

三、解答题

18. 计算： ${(- 1)}^{2022} + | 1 - \sqrt{2} | - \sqrt[3]{27}$

查看试题解析
19. 解不等式组： ${\begin{matrix} \end{matrix} \begin{matrix} 2 x + 1 > x \\ \frac{x + 5}{2} - x \geq 1 \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
20. 为积极落实国家“双减”政策，某学校举办读书节，购买了一批课外读物，为使购买的课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了名同学？（直接填答案）

(2)、 $m$ = ， $n$ = ．（直接填答案）

(3)、根据调查的结果，请你给学校购买课外读物提供两条合理化建议．

查看试题解析
21. 在平面直角坐标系中，ABC三个顶点的位置如图（每个小正方形的边长均为1）：

(1)、请画出△ABC沿 $x$ 轴向右平移3个单位长度，再沿 $y$ 轴向上平移2个单位长度后的 $△ A^{'} B^{'} C^{'}$ (其中 $A^{'} 、 B^{'} 、 C^{'}$ 分别是A、B、C的对应点，不写画法)；

(2)、直接写出 $A^{'} 、 B^{'} 、 C^{'}$ 三点的坐标；

(3)、直接写出△ABC的面积．

查看试题解析
22. 已知：如图EF∥CD，∠1＋∠2=180°．

(1)、求证：GD∥CA；

(2)、若CD平分∠ACB，DG平分∠CDB，且∠A=40°，求∠CGD的度数．

查看试题解析
23. 某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车，恰好全部坐满，已知每辆大客车的乘客座位数比小客车多17个．

(1)、求每辆大客车和每辆小客车的乘客座位数；

(2)、由于最后参加活动的人数增加了30人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，且所有参加活动的师生都有座位，求租用小客车数量的最大值．

查看试题解析
24. 如图，已知 $A M ∥ B N$ ，点P是射线 $A M$ 上一动点（不与点A重合）． $B C 、 B D$ 分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线 $A M$ 于点 $C ， D$ ．

(1)、【问题解决】如果 $∠ A = 60 °$ ，求 $∠ A B N 、 ∠ C B D$ 的度数；
下面是小明同学的解答，请你按小明同学的解答思路注明依据及补充完成解答过程，也可以按自己的思路重新完整的解答．
解： $∵ A M ∥ B N$ ，
$∴ ∠ A B N + ∠ A = 180 °$ ，（      ）
$∵ ∠ A = 60 °$ ，
$∴ ∠ A B N = ∠ A B P + ∠ P B N =$       ▲ ，
$∵ B C$ 平分 $∠ A B P ， B D$ 平分 $∠ P B N$ ，
$∴ ∠ A B P = 2 ∠ C B P ， ∠ P B N = 2 ∠ D B P$ ，
$∴ 2 ∠ C B P + 2 ∠ D B P = ∠ A B P + ∠ P B N = ∠ A B N =$       ▲ ，
则 $∠ C B P + ∠ D B P =$       ▲ ，
$∴ ∠ C B D = ∠ C B P + ∠ D B P =$       ▲ ．

(2)、【探究发现】探究 $∠ C B D$ 与 $∠ A$ 的数量关系．

(3)、当点P运动时， $∠ A P B$ 与 $∠ A D B$ 之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律．

查看试题解析
25. 如图①，在平面直角坐标系中，A(a，0)，C(b，2)，且满足 (a+2)²+ $\sqrt{b - 2}$ =0，过C作CB⊥x轴于B．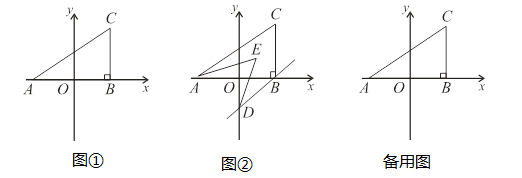

(1)、直接写出三角形ABC的面积；

(2)、如图②，若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数；

(3)、在y轴上是否存在点P，使得三角形ACP和三角形ABC的面积相等？若存在，求出P点的坐标；若不存在，请说明理由．

查看试题解析