广东省茂名市电白区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 一个长方形的面积为4a2﹣6ab+2a,它的长为2a,则宽为( )A、2a﹣3b B、4a﹣6b C、2a﹣3b+1 D、4a﹣6b+22. 在同一平面内两两相交的三条直线,若最多有m个交点,最少有n个交点,则m+n等于( )A、1 B、2 C、3 D、43. 赵先生手中有一张记录他从出生到24周岁期间的身高情况表(如下):
年龄x/岁
0
3
6
9
12
15
18
21
24
身高h/cm
48
100
130
140
150
158
165
170
170.4
下列说法中错误的是( )
A、赵先生的身高增长速度总体上先快后慢 B、赵先生的身高在21岁以后基本不长了 C、赵先生的身高从0岁到12岁平均每年增高12.5cm D、赵先生的身高从0岁到24岁平均每年增高5.1cm4. 如图, , , 于 点, 于 点, , , 则 的长为 ( ) A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 已知x y = 9,x-y=-3,则x2+3xy+y2的值为 ( )A、27 B、9 C、54 D、187. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球,这些小球上分别标有数字-1、0、2和3.从中随机地摸取一个小球,则这个小球所标数字是正数的概率为( )A、 B、 C、 D、8. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 已知x y = 9,x-y=-3,则x2+3xy+y2的值为 ( )A、27 B、9 C、54 D、187. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球,这些小球上分别标有数字-1、0、2和3.从中随机地摸取一个小球,则这个小球所标数字是正数的概率为( )A、 B、 C、 D、8. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )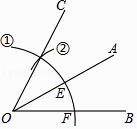 A、以点F为圆心,OE长为半径画弧 B、以点F为圆心,EF长为半径画弧 C、以点E为圆心,OE长为半径画弧 D、以点E为圆心,EF长为半径画弧9. 为应对越来越复杂的交通状况,某城市对其道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路(米)与时间(天)的关系的大致图象是( )A、
A、以点F为圆心,OE长为半径画弧 B、以点F为圆心,EF长为半径画弧 C、以点E为圆心,OE长为半径画弧 D、以点E为圆心,EF长为半径画弧9. 为应对越来越复杂的交通状况,某城市对其道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路(米)与时间(天)的关系的大致图象是( )A、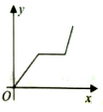 B、
B、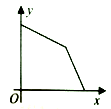 C、
C、 D、
D、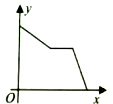 10. 如图, , , . 给出下列结论:①;②;③;④ . 其中正确的结论是( )
10. 如图, , , . 给出下列结论:①;②;③;④ . 其中正确的结论是( )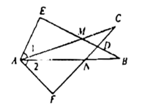 A、②③ B、①②③ C、①③ D、①②11. 如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点 处,点B落在点 处,若 则图中 的度数为( )
A、②③ B、①②③ C、①③ D、①②11. 如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点 处,点B落在点 处,若 则图中 的度数为( )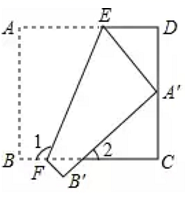 A、40° B、45° C、50° D、60°12. 设a=355 , b=444 , c=533 , 则a、b、c的大小关系是( )A、c<a<b B、a<b<c C、b<c<a D、c<b<a
A、40° B、45° C、50° D、60°12. 设a=355 , b=444 , c=533 , 则a、b、c的大小关系是( )A、c<a<b B、a<b<c C、b<c<a D、c<b<a二、填空题
-
13. 已知 , , 则 .14. 若 , , 则 .15. 四张质地、大小相同的卡片上,分别画上如图所示的四个图形.在看不到图形的情况下从中任意抽取一张,则抽取的卡片是轴对称图形的概率为 .
 16. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是 .
16. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是 .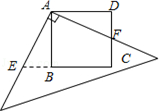 17. 如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形……这样继续摆下去,当摆出第()个正三角形时,共用了木棒m根,则m与n之间的关系式为 .
17. 如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形……这样继续摆下去,当摆出第()个正三角形时,共用了木棒m根,则m与n之间的关系式为 . 18. 我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45°,那么该等腰三角形的顶角等于 .
18. 我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45°,那么该等腰三角形的顶角等于 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,某校有一块长为米,宽为米的长方形空地,中间是边长米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
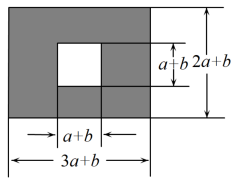 (1)、用含 , 的代数式表示需要硬化的面积并化简;(2)、当 , 时,求需要硬化的面积.21. 如图,在三角形ABC中,点D是BC上的中点,连接AD并延长到点E,使 ,连接CE.
(1)、用含 , 的代数式表示需要硬化的面积并化简;(2)、当 , 时,求需要硬化的面积.21. 如图,在三角形ABC中,点D是BC上的中点,连接AD并延长到点E,使 ,连接CE.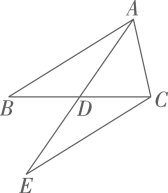 (1)、求证:(2)、若 的面积为5,求 的面积.22. 如图,中,BD平分 , , ∠3=∠C,求的度数.
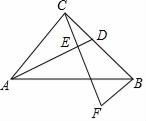
(1)、求证:(2)、若 的面积为5,求 的面积.22. 如图,中,BD平分 , , ∠3=∠C,求的度数.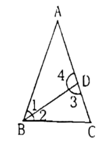 23. 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC , 点D是BC的中点,CE⊥AD , 垂足为点E , BF∥AC交CE的延长线于点F .
23. 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC , 点D是BC的中点,CE⊥AD , 垂足为点E , BF∥AC交CE的延长线于点F .求证:AC=2BF .
 24. 如图1,在中, , 直线过点 , 且 , 点是直线上一点,不与点重合.
24. 如图1,在中, , 直线过点 , 且 , 点是直线上一点,不与点重合.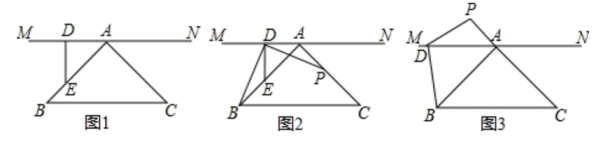 (1)、若点是图1中线段上一点,且 , 判断线段与的位置关系,并说明理由;(2)、请在下面的两题中任选题解答.
(1)、若点是图1中线段上一点,且 , 判断线段与的位置关系,并说明理由;(2)、请在下面的两题中任选题解答.:如图2,在(1)的条件下,连接, 过点作交线段于点 , 请判断线段与的数量关系,并说明理由;
:如图3,在图1的基础上,改变点的位置后,连接 , 过点作交线段的延长线于点 , 请判断线段与的数量关系,并说明理由.
我选择: ▲