广东省揭阳市普宁市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. “致中和，天地位焉，万物育焉”，对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光，在下列标识或简图中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{6} + x^{6} = 2 x^{12}$ B、 $a^{2} \cdot a^{4} = a^{6}$ C、 $(x - y)^{2} = x^{2} - 2 x y - y^{2}$ D、 $(a + b) (a - b) = a^{2} + b^{2}$

查看试题解析
3. 如图，下列条件中不能判断a $∥$ b的是（）．

A、∠2＝∠6 B、∠3+∠5＝180° C、∠4+∠6＝180° D、∠1＝∠4

查看试题解析
4. 下列事件是必然事件的是（）

A、路口遇到红灯 B、掷一枚硬币正面朝上 C、三角形的两边之和大于第三边 D、异号两数之和小于零

查看试题解析
5. 如图，在△ABC和△DEF中，点B、F、C、D在同一条直线上，已知∠A＝∠D，AB＝DE，添加以下条件，不能判定△ABC≌△DEF的是（）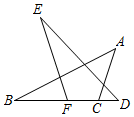

A、∠B＝∠E B、AC＝DF C、∠ACD＝∠BFE D、BC＝EF

查看试题解析
6. 将边长分别为 $a + b$ 和a-b的两个正方形摆放成如图所示的位置，则阴影部分的面积化简后的结果（）

A、 $a - b$ B、 $a + b$ C、2ab D、4ab

查看试题解析
7. 如图，是由两个大小完全相同的圆柱形容器在中间连通而成的可以盛水的器具，现匀速地向容器A中注水，则容器A中水面上升的高度h随时间t变化的大致图象是（）

A、 B、 C、 D、

查看试题解析
8. 如图，AB∥CD ，直线 EF 分别交 AB ， CD 于 M ， N 两点，将一个含有 45°角的直角三角尺按如图所示的方式摆放，若∠EMB＝75°，则∠PNM 等于（）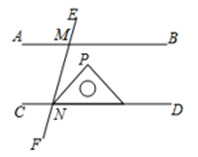

A、15° B、25° C、30° D、45°

查看试题解析
9. 某木材市场上木棒规格与对应价格如下表：
规格
1m
2m
3m
4m
5m
6m
价格(元/根)
10
15
20
25
30
35
小明的爷爷要做一个三角形的木架养鱼用，现有两根长度分别为3m和5m的木棒，还需要到该木材市场上购买一根木棒．则小明的爷爷至少带的钱数应为（）

A、10元 B、15元 C、20元 D、25元

查看试题解析

二、解答题

10. 如图，在△ABC中，AP平分∠BAC交BC于点P，过点P作PR⊥AB垂足为R，PS⊥AC垂足为S，在AC上取一点Q，使AQ＝PQ．则①PR＝PS，②AS＝AR，③ $Q P ∥ A R$ ， ④△BRP≌△CSP．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 计算： $5^{- 1} \div 5^{- 3} + (- 1)^{2022} - {(\frac{1}{2})}^{- 1} + (3.14 - π)^{0}$

查看试题解析
12. 先化简，再求值：
$[{(x + 2 y)}^{2} - (x + y) (3 x - y) - 5 y^{2}] \div 2 x$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$

查看试题解析
13. 如图，已知∠1＝∠2，∠3＝∠4，求证： $B C ∥ E F$ ．完成推理填空：
证明：∵∠1＝∠2（已知），
∴ $A C$ $∥$             ▲        ，（   ）
∴∠3＝∠5（   ）
又∵∠3＝∠4（已知），
∴∠5＝∠            ▲       （   ），
∴ $B C ∥ E F$ （   ）

查看试题解析
14. 如图，在△ABC中，∠B＝30°，∠C＝40°.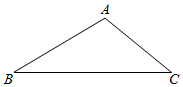

(1)、尺规作图：①作边AB的垂直平分线交BC于点D；
②连接AD，作∠CAD的平分线交BC于点E；（要求：保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求∠DAE的度数.

查看试题解析
15. 一个不透明的袋中装有红、黄、白三种颜色的球共10个，它们除了颜色外完全相同，其中黄球个数比白球个数的3倍少2个，从袋中摸出一个球是黄球的概率为0.4.

(1)、求袋中红、黄、白三种颜色的球的个数；

(2)、向袋中放入若干个红球，使摸出一个球是红球的概率为0.7，求放入红球的个数；

(3)、在（2）的条件下，求摸出一个球是白球的概率.

查看试题解析
16. 小颖和小强上山游玩，小颖乘坐缆车，小强步行，两人相约在山顶的缆车终点会和，已知小强行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小强出发后50分才乘上缆车，缆车的平均速度为180米/分，若图中的折线表示小强在整个行走过程中的路程（米）与出发时间（分）之间的关系的图象，请回答下列问题.

(1)、小强行走的总路程是米，他途中休息了分；

(2)、分别求出小强在休息前和休息后所走的两段路程的速度；

(3)、当小颖到达缆车终点时，小强离缆车终点的路程是多少？

查看试题解析
17. 如图，将边长为 $(a + b)$ 的正方形剪出两个边长分别为a，b的正方形（阴影部分）．
观察图形，解答下列问题：

(1)、根据题意，用两种不同的方法表示阴影部分的面积，即用两个不同的代数式表示阴影部分的面积．方法1：，方法2：；

(2)、从（1）中你能得到怎样的等式？；

(3)、运用你发现的结论，解决下列问题：
①已知x＋y＝6， $\frac{1}{2} x y = 2$ ，求 $x^{2} + y^{2}$ 的值；
②已知 ${(2022 - x)}^{2} + {(x - 2021)}^{2} = 9$ ，求 $(2022 - x) (x - 2021)$ 的值．

查看试题解析
18. 如图，在△ABC中，点M、N分别为线段BC、AC上的动点，当M运动到线段BC的中点时有AM⊥BC．

(1)、证明：AB＝AC；

(2)、设线段AB的中点为D，当AB＝14cm，BC＝13cm时，若动点M从B点出发，以2cm/s的速度沿线段BC由B点向C点运动，动点N从C点出发匀速沿线段CA由C点向A点运动，动点M出发1秒后动点N才出发，当点N的运动速度为多少时，能够使△BMD与△CNM全等？

(3)、若AB⊥AC，当BN平分∠ABC时，延长BN至点E使得AE＝AB，∠CAE的角平分线交BE于F，证明：BN＝2EF．

查看试题解析

三、填空题

19. 新冠病毒是病毒的一种，病毒的体积微小，一般在电镜下才能见到.在病毒中，有一种病毒直径约0.000 000 021m，请用科学记数法把数0.000 000 021m表示出来.

查看试题解析
20. 一个小球在光滑度相同的地板上（如图）自由滚动，并随机地停留在某块方砖上，则它最终停留在黑砖上的概率是．

查看试题解析
21. 如图，OP平分∠MON，PA⊥ON于点A，若PA＝3，则点P到射线OM的距离是．

查看试题解析
22. 如图， $R t △ A B C$ 中， $∠ B = 90 ° ， A B = 3 ， B C = 4$ ，将 $△ A B C$ 折叠，使点 $C$ 与 $A$ 重合，得折痕 $D E$ ，则 $△ A B E$ 的周长等于．

查看试题解析
23. 如图所示，AB $//$ DE，∠1＝130°，∠2＝36°，则∠3等于.

查看试题解析
24. 如图，在△ABC中，∠C＝90°，点D是边BC上一动点，若AC＝4，BC＝15，CD＝x，则△ABD的面积S与x之间的函数关系式为．

查看试题解析
25. 如图，∠A＝∠B＝90°，AB＝60，E，F 分别为线段 AB 和射线 BD 上的一点，若点 E 从点 B 出发向点 A 运动，同时点 F 从点 B 出发向点 D 运动，二者速度之比为 3：7，运动到某时刻同时停止，在射线 AC 上取一点 G，使△AEG 与△BEF 全等，则 AG 的长为.

查看试题解析

规格	1m	2m	3m	4m	5m	6m
价格(元/根)	10	15	20	25	30	35