广东省广州市增城区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 在2022北京冬奥会上以熊猫为原型的吉祥物“冰墩墩”成了全网“顶流”,通过平移吉祥物“冰墩墩”可以得到的图形是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 2. 16的平方根是( )A、 4 B、±4 C、±2 D、±83. 在实数 , 2, , 中,无理数是( )A、-1 B、2 C、 D、4. 抽样调查放学时段,学校附近某路口车流量情况的样本中,下列最合适的是( )A、抽取一月份第一周为样本 B、抽取任意一天为样本 C、选取每周日为样本 D、每个季节各选两周作为样本5. 如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
2. 16的平方根是( )A、 4 B、±4 C、±2 D、±83. 在实数 , 2, , 中,无理数是( )A、-1 B、2 C、 D、4. 抽样调查放学时段,学校附近某路口车流量情况的样本中,下列最合适的是( )A、抽取一月份第一周为样本 B、抽取任意一天为样本 C、选取每周日为样本 D、每个季节各选两周作为样本5. 如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )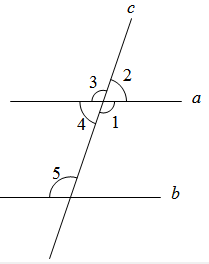 A、∠3=∠5 B、∠1=∠5 C、∠4+∠5=180° D、∠2=∠46. 如图,ABCD,EF分别交AB,CD于E,F,EG⊥AB,已知∠FEG=25°,则∠CFE的度数是( )
A、∠3=∠5 B、∠1=∠5 C、∠4+∠5=180° D、∠2=∠46. 如图,ABCD,EF分别交AB,CD于E,F,EG⊥AB,已知∠FEG=25°,则∠CFE的度数是( )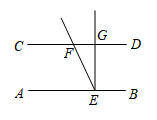 A、125° B、130° C、155° D、115°7. 如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A、125° B、130° C、155° D、115°7. 如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )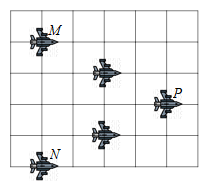 A、(﹣1,﹣3) B、(3,﹣1) C、(﹣1,3) D、(3,0)8. 不等式组的解集在数轴上表示为( )A、
A、(﹣1,﹣3) B、(3,﹣1) C、(﹣1,3) D、(3,0)8. 不等式组的解集在数轴上表示为( )A、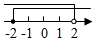 B、
B、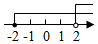 C、
C、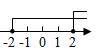 D、
D、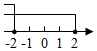 9. 如图,七个相同的小长方形组成一个大长方形 , 若 , 则长方形的周长为( )
9. 如图,七个相同的小长方形组成一个大长方形 , 若 , 则长方形的周长为( )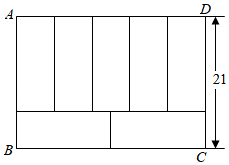 A、100 B、102 C、104 D、10610. 定义新运算:对于任意实数a,b都有 , 等式右边是常用的乘法和减法运算.规定,若 , , 则的值为( )A、-2 B、-4 C、-7 D、-11
A、100 B、102 C、104 D、10610. 定义新运算:对于任意实数a,b都有 , 等式右边是常用的乘法和减法运算.规定,若 , , 则的值为( )A、-2 B、-4 C、-7 D、-11二、填空题
-
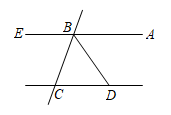
11. 在我市体育馆一侧的座位上,6排3号记为(6,3),则5排8号记为 .12. 计算: .13. 如图, , BD平分∠ABC, , 则 .
 14. 已知x、y满足方程组 , 则 .15. 在一个样本中有50个数据,它们分别落在5个组内,已知第一、二、三、四、五组数据的个数分别有 ,则第四组的频数为.16. 在平面直角坐标系中, , , , , , , …,按此规律排列,则点的坐标是 .
14. 已知x、y满足方程组 , 则 .15. 在一个样本中有50个数据,它们分别落在5个组内,已知第一、二、三、四、五组数据的个数分别有 ,则第四组的频数为.16. 在平面直角坐标系中, , , , , , , …,按此规律排列,则点的坐标是 .
三、解答题
-
17. 计算:.18. 解方程组:19. 解不等式组: , 并把解集在数轴上表示出来.
 20. 如图,已知 , .
20. 如图,已知 , .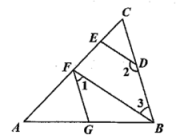 (1)、试判断BF与DE的位置关系,并说明理由;(2)、若 , , 求∠AFG的度数.21. 2021年7月以来,教育部相继出台文件,实施义务教育“双减”政策,某校开展课后延时服务,从篮球、绘画、乐器、手工四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成以下两幅不完整的统计图,根据图中提供的信息解答下列问题:
(1)、试判断BF与DE的位置关系,并说明理由;(2)、若 , , 求∠AFG的度数.21. 2021年7月以来,教育部相继出台文件,实施义务教育“双减”政策,某校开展课后延时服务,从篮球、绘画、乐器、手工四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成以下两幅不完整的统计图,根据图中提供的信息解答下列问题: (1)、补全条形统计图.(2)、若该校爱好绘画的学生共有900名,则该校学生总数大约有多少名?22. 如图,在平面直角坐标系中, , , 点P的坐标是 .
(1)、补全条形统计图.(2)、若该校爱好绘画的学生共有900名,则该校学生总数大约有多少名?22. 如图,在平面直角坐标系中, , , 点P的坐标是 .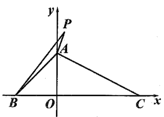 (1)、直接写出顶点A,C的坐标;(2)、连接PA,PB,求的面积.23. 截至2022年3月27日,全国累计报告接种新型冠状病毒疫苗超过32亿剂次,为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1万剂疫苗的平均成本为80万元.(1)、该公司每周每个大车间生产疫苗万剂, 每个小车间生产疫苗万剂;(2)、若所有10个车间全部投入生产,且每周生产的疫苗不少于135 万剂,请问共有几种投入方案,请列出所有正确的方案,并求出每周生产疫苗的总成本最小值.24. 在平面直角坐标系中(单位长度为1cm),已知点 , , 且 .(1)、分别求m,n的值;(2)、若点E是第一象限内一点,且轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
(1)、直接写出顶点A,C的坐标;(2)、连接PA,PB,求的面积.23. 截至2022年3月27日,全国累计报告接种新型冠状病毒疫苗超过32亿剂次,为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1万剂疫苗的平均成本为80万元.(1)、该公司每周每个大车间生产疫苗万剂, 每个小车间生产疫苗万剂;(2)、若所有10个车间全部投入生产,且每周生产的疫苗不少于135 万剂,请问共有几种投入方案,请列出所有正确的方案,并求出每周生产疫苗的总成本最小值.24. 在平面直角坐标系中(单位长度为1cm),已知点 , , 且 .(1)、分别求m,n的值;(2)、若点E是第一象限内一点,且轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.①经过几秒时,PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是10cm2 , 求此时点P的坐标.
25. 已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.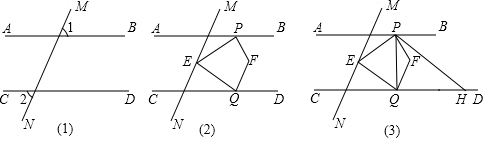 (1)、求证:AB∥CD;(2)、如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)、如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.
(1)、求证:AB∥CD;(2)、如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)、如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.