广东省广州市越秀区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 下列四个数中,属于无理数的是( )A、 B、0.2 C、 D、2. 下列调查中,适宜采用全面调查(普查)方式的是( )A、调查某电视节目的收视率 B、调查乘坐飞机的旅客是否携带了违禁物品 C、调查某品牌冰箱的使用寿命 D、调查市场上冷冻食品的质量情况3. 若m<n,则下列各式一定正确的是( )A、 B、 C、 D、4. 在平面直角坐标系xOy中,点在第二象限,则m的取值范围是( )A、 B、 C、 D、5. 如图,直线AB,CD相交于点O, , 垂足为O,若 , 则的度数为( )
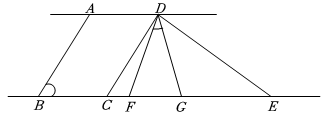
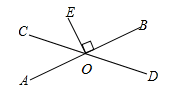 A、115° B、120° C、125° D、130°6. 在下列命题中,假命题是( )A、如果两个角是互为邻补角,那么这两个角互补 B、如果两条直线被第三条直线所截,那么同位角相等 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、如果两条直线都与第三条直线平行,那么这两条直线也互相平行7. 如图,在三角形ABC中, , 把三角形ABC平移到三角形DEF的位置,点B、E、C、F在同一直线上, , , 则下列结论中错误的是( )
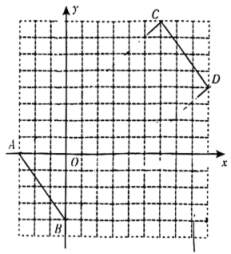
A、115° B、120° C、125° D、130°6. 在下列命题中,假命题是( )A、如果两个角是互为邻补角,那么这两个角互补 B、如果两条直线被第三条直线所截,那么同位角相等 C、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、如果两条直线都与第三条直线平行,那么这两条直线也互相平行7. 如图,在三角形ABC中, , 把三角形ABC平移到三角形DEF的位置,点B、E、C、F在同一直线上, , , 则下列结论中错误的是( )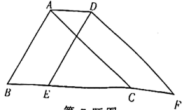 A、 B、 C、 D、8. 一服装厂用136米布料生产玩偶A与玩偶B(不考虑布料的损耗),已知每米布料可做1个玩偶A或3个玩偶B,玩偶B数量是玩偶A数量的两倍.设用x米布料做玩偶A,用y米布料做玩偶B,则下列方程组正确的是( )A、 B、 C、 D、9. 在平面直角坐标系xOy中,点 , 点 , 点C在y轴上,若三角形ABC的面积为3,则点C的坐标是( )A、 B、 C、或 D、或10. 已知关于x、y的二元一次方程组其中 , 给出下列四个结论:①当时,方程组的解也是方程的解;②当时,x、y的值互为相反数;③若 , 则;④是方程组的解.其中正确的结论有( )个.A、1 B、2 C、3 D、4
A、 B、 C、 D、8. 一服装厂用136米布料生产玩偶A与玩偶B(不考虑布料的损耗),已知每米布料可做1个玩偶A或3个玩偶B,玩偶B数量是玩偶A数量的两倍.设用x米布料做玩偶A,用y米布料做玩偶B,则下列方程组正确的是( )A、 B、 C、 D、9. 在平面直角坐标系xOy中,点 , 点 , 点C在y轴上,若三角形ABC的面积为3,则点C的坐标是( )A、 B、 C、或 D、或10. 已知关于x、y的二元一次方程组其中 , 给出下列四个结论:①当时,方程组的解也是方程的解;②当时,x、y的值互为相反数;③若 , 则;④是方程组的解.其中正确的结论有( )个.A、1 B、2 C、3 D、4二、填空题
-
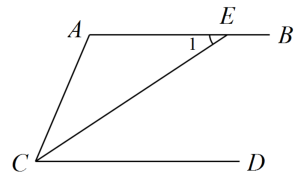
11. 已知方程是关于x、y的二元一次方程,则n= .12. 若某正数的两个不等的平方根分别是与 , 则 .13. 小明爸爸种了荔枝树100株,现进入收获期,收获时先随意采摘5株树上的荔枝,称得每株树上的荔枝重量如下(单位:千克):100,98,102,103,97.若荔枝售价为每千克20元,估计这年小明爸爸卖荔枝的收入为元.14. 如图,已知 , CE平分交AB于点E, , 则的度数是 .
 15. 在平面直角坐标系xOy中,点M的坐标是(1,2),轴, , 则点N的坐标是 .16. 如果关于的一元一次不等式组的解集为 , 则的立方根为 .
15. 在平面直角坐标系xOy中,点M的坐标是(1,2),轴, , 则点N的坐标是 .16. 如果关于的一元一次不等式组的解集为 , 则的立方根为 .三、解答题
-
17.(1)、求x的值: .(2)、计算: .18. 解下列方程组:(1)、;(2)、 .19. 解下列不等式组,并把解集在数轴上表示出来:
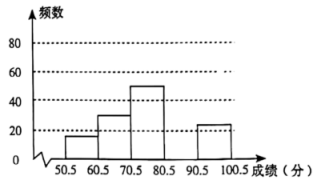
 20. 羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩(得分取正整数,满分为100分)进行统计分析,请根据下列尚未完成的统计图表,解答问题.
20. 羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩(得分取正整数,满分为100分)进行统计分析,请根据下列尚未完成的统计图表,解答问题.组别
分数段
频数
百分比
一
50.5~60.5
16
8%
二
60.5~70.5
30
15%
三
70.5~80.5
50
25%
四
80.5~90.5
a
40%
五
90.5~100.5
24
12%
 (1)、本次抽样调查的样本容量为 ▲ , 表中 ▲ , 并补全频数分布直方图;(2)、若把各组的分数段所占的百分比绘制成扇形统计图,则第三组对应的扇形圆心角的度数是;(3)、该校一共组织2000名学生参加阅读大赛,若抽取的样本具有较好的代表性,且成绩超过80分为优秀,请估计该校学生中阅读能力优秀的约有多少人?21. 2022年北京冬奥会、冬残奥会的纪念品得到广大民众的喜爱,某校想要购买A型、B型两种纪念品.已知购买2件A型纪念品和1件B型纪念品共需150元;购买3件A型纪念品和2件B型纪念品共需245元.(1)、求A型纪念品和B型纪念品的单价;(2)、学校现需一次性购买A型纪念品和B型纪念品共100个,要求购买的总费用不超过5000元,则最多可以购买多少个A型纪念品?
(1)、本次抽样调查的样本容量为 ▲ , 表中 ▲ , 并补全频数分布直方图;(2)、若把各组的分数段所占的百分比绘制成扇形统计图,则第三组对应的扇形圆心角的度数是;(3)、该校一共组织2000名学生参加阅读大赛,若抽取的样本具有较好的代表性,且成绩超过80分为优秀,请估计该校学生中阅读能力优秀的约有多少人?21. 2022年北京冬奥会、冬残奥会的纪念品得到广大民众的喜爱,某校想要购买A型、B型两种纪念品.已知购买2件A型纪念品和1件B型纪念品共需150元;购买3件A型纪念品和2件B型纪念品共需245元.(1)、求A型纪念品和B型纪念品的单价;(2)、学校现需一次性购买A型纪念品和B型纪念品共100个,要求购买的总费用不超过5000元,则最多可以购买多少个A型纪念品?