广东省广州市番禺区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列点在第三象限的是（）

A、（1，1） B、（﹣1，1） C、（﹣1，﹣1） D、（1，﹣1）

查看试题解析
2. 下列说法正确的是（）

A、1的平方根是1 B、4的算术平方根是2 C、 $\pm 2$ 是4的立方根 D、0无立方根

查看试题解析
3. 四个实数－2，0，－ $\sqrt{2}$ ， 1中，最小的实数是（）

A、－ $\sqrt{2}$ B、0 C、－2 D、1

查看试题解析
4. 以下调查中，最适合用来全面调查的是（）

A、调查柳江流域水质情况 B、了解全国中学生的心理健康状况 C、了解全班学生的身高情况 D、调查春节联欢晚会收视率

查看试题解析
5. 如图，下面推理中，正确的是（）

A、∵∠DAE＝∠D，∴AD∥BC B、∵∠DAE＝∠B，∴AB∥CD C、∵∠B+∠C＝180°，∴AB∥CD D、∵∠D+∠B＝180°，∴AD∥BC

查看试题解析
6. 如图，直线a、b被直线c所截， $a / / b$ ，若∠2=50°，则∠1等于（）

A、120° B、130° C、140° D、150°

查看试题解析
7.
为了了解我市某学校“书香校园”的建设情况，检查组在该校随机抽取40名学生，调查了解他们一周阅读课外书籍的时间，并将调查结果绘制成如图所示的频数分布直方图（每小组的时间包含最小值，不包含最大值），根据图中信息估计该校学生一周课外阅读时间不少于4小时的人数占全校人数的百分数约等于（　　）

A、50% B、55% C、60% D、65%

查看试题解析
8. 如图，已知数轴上的点 $A 、 B 、 C 、 D$ 分别表示数 $- 2 、 1 、 2 、 3$ ，则表示数 $3 - \sqrt{5}$ 的点 $P$ 应落在线段（）

A、 $A O$ 上 B、 $O B$ 上 C、 $B C$ 上 D、 $C D$ 上

查看试题解析
9. 如果不等式组 ${\begin{array}{l} 2 x + 5 ＞ 3 x + 3 \\ x ＜ m \end{array}$ 的解集是x＜2，那么m的取值范围是（）.

A、m=2 B、m＞2 C、m≥2 D、m＜2

查看试题解析
10. 定义新运算：对于任意实数a，b都有 $a \oplus b = a p + b q$ ，等式右边是常用的乘法和减法运算．规定，若 $3 \oplus 2 = 5$ ， $1 \oplus (- 2) = - 1$ ，则 $(- 3) \oplus 1$ 的值为（）

A、－2 B、－4 C、－7 D、－11

查看试题解析

二、填空题

11. 在平面直角坐标系中，点P（﹣1，2）向右平移3个单位长度再向上平移1个单位长度得到的点的坐标是．

查看试题解析
12. 如图，O是直线AB上一点，∠COB=30°，则∠1=.

查看试题解析
13. 一个班有40名学生，在期末体育考核中，成绩为优秀的有18人，在扇形统计图中，代表体育成绩优秀的扇形圆心角的度数是．

查看试题解析
14. 若实数a、b满足|a+2|+ $\sqrt{b - 4}$ =0，则 $\frac{a^{2}}{b}$ = ．

查看试题解析
15. 已知AB//y轴，A点的坐标为(3，2)，并且AB=5，则B的坐标为．

查看试题解析
16. 如图，如果 $A B$ // $C D$ // $E F$ ，那么 $∠ B A C + ∠ A C E + ∠ C E F =$ 度．

查看试题解析

三、解答题

17. 把下面的说理过程补充完整：
如图，已知： $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ，试判断 $∠ A E D$ 与 $∠ C$ 的关系，并说明理由．
解： $∠ A E D = ∠ C$ ．
理由：∵ $∠ 1 + ∠ A D G = 180 °$ （平角定义）， $∠ 1 + ∠ 2 = 180 °$ （已知）．
∴ $∠ 2 = ∠ A D G$ （    ）
∴ $E F$ // $A B$ （    ）
∴ $∠ 3 = ∠ A D E$ （    ）
∵ $∠ 3 = ∠ B$ （已知）
∴ $∠ B = ∠ A D E$ （等量代换）
∴ $D E$ // $B C$ （同位角相等两直线平行）
∴ $∠ A E D = ∠ C$ （    ）

查看试题解析
18. 解方程组： ${\begin{array}{l} 2 x - 5 y = - 3 \\ - 4 x + y = - 3 \end{array}$

查看试题解析
19. 解不等式组 ${\begin{array}{l} \frac{x}{3} - (x - 2) \geq 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{array}$ ，并利用数轴表示出该不等式组的解集．x有正整数值使此不等式组成立吗？如有，请写出此值；否则，说明理由．

查看试题解析

20. 文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办，引起了世界人民的极大关注．某市一研究机构为了了解10～60岁年龄段市民对本次大会的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图，如下所示：

组别	年龄段	频数（人数）
第1组	$10 \leq x < 20$	5
第2组	$20 \leq x < 30$	$a$
第3组	$30 \leq x < 40$	35
第4组	$40 \leq x < 50$	20
第5组	$50 \leq x < 60$	15

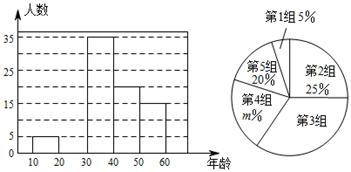(1)、请直接写出

a =

，

m =

，第3组人数在扇形统计图中所对应的圆心角是度．

(2)、请补全上面的频数分布直方图；

(3)、假设该市现有10～60岁的市民300万人，问40～50岁年龄段的关注本次大会的人数约有多少？

查看试题解析

21. 如图，已知： $C D ⊥ A B$ 于D， $D E$ // $B C$ ， $E F ⊥ A B$ 于F，求证： $∠ F E D = ∠ B C D$ ．（要求：证明中的每一步推理都要有根据）

查看试题解析
22. △ABC与△A₁B₁C₁在平面直角坐标系中的位置如图所示．

(1)、分别写出下列各点的坐标：A、B、C；

(2)、△ABC是由△A₁B₁C₁经过怎样的平移得到的?

(3)、若点P（x，y）是△ABC内部一点，求△A₁B₁C₁内部的对应点P₁的坐标；

(4)、求△ABC的面积．

查看试题解析
23. 把一部分书分给几名同学，如果每人分3本，则余8本；如果前面的每名同学分5本，那么最后一人就分不到3本（包含分不到书的情况），这些书有多少本？共有多少人？

查看试题解析
24. 某电脑公司有A型、B型、C型三种型号电脑，其中A型每台6000元，B型每台4000元，C型每台2500元，某中学现有资金100500元，计划全部用于从这家电脑公司购进36台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择，并说明理由.

查看试题解析
25. 如图，已知直线 $A B$ // $C D$ ，点M在直线AB，CD之间，且 $M N$ // $C D$ ．

(1)、如图1，若 $∠ C = α$ ， $∠ B = β$ ，请用 $α$ 、 $β$ 表示 $∠ C M B$ ；

(2)、如图2，NB、PN所在直线分别平分 $∠ A B M$ 、 $∠ D C M$ ，且 $C M$ // $N B$ ， $∠ P = 90 °$ ，求 $∠ D C M ： ∠ C M B ： ∠ A B M$ 的值．

查看试题解析