广东省佛山市顺德区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 空气的密度是 $0.001293 g / c m^{3}$ ．将0.001293用科学记数法表示为（）

A、 $0.1293 \times 1 0^{- 3}$ B、 $1.293 \times 1 0^{- 3}$ C、 $1.293 \times 1 0^{- 4}$ D、 $12.93 \times 1 0^{- 4}$

查看试题解析
2. 下列图形不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一个不透明的盒子中装有1个红球、2个黄球和3个蓝球，这些球除了颜色外无其他差别．随机摸出一个小球，恰好是黄球的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{3})}^{3} = a^{6}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a^{2} b)}^{3} = a^{6} b^{3}$

查看试题解析
5. 经过有交通信号灯的路口遇到绿灯，这个事件是（）

A、必然事件 B、不可能事件 C、随机事件 D、以上说法都不对

查看试题解析
6. 如果一个角是 $60 °$ ，那么它的补角的度数是（）

A、 $30 °$ B、 $60 °$ C、 $120 °$ D、 $140 °$

查看试题解析
7. 如图，下列条件能判定 $a ∥ b$ 的是（）

A、∠1＝∠2 B、∠2＝∠4 C、∠1＝∠4 D、∠1＋∠3＝180°

查看试题解析
8. 已知 $a^{m} = 8$ ， $a^{n} = 2$ ，则 $a^{m - n} =$ （）

A、4 B、6 C、10 D、16

查看试题解析
9. 如图，已知AC＝AD，要使△ABC≌△ABD，还需要添加一个条件，给出下列条件：①∠1＝∠2，②∠C＝∠D，③BC＝BD，其中符合要求的是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析
10. 七巧板起源于我国宋代，后流传于世界各国．数学兴趣小组在综合与实践课上用一张面积为 $100 c m^{2}$ 的正方形纸片先制作了一副如图1所示的七巧板，再拼成如图2所示的作品，则图2中①和②的面积之和是（）

A、 $12.5 c m^{2}$ B、 $18.75 c m^{2}$ C、 $25 c m^{2}$ D、 $37.5 c m^{2}$

查看试题解析

二、填空题

11. 计算： $3^{- 2}$ =.

查看试题解析
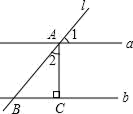
12. 计算： ${(2 x + 1)}^{2} =$ ．

查看试题解析
13. 如图，直线a∥b，直线1与a，b分别交于点A，B，过点A作AC⊥b于点C，若∠1＝50°，则∠2的度数为．

查看试题解析
14. 如图，正方形边长为12cm，在四个角分别剪去全等的等腰直角三角形．当三角形的直角边由小变大时，阴影部分的面积变化如下表所示：
三角形的直角边/cm
1
2
3
4
5
6
阴影部分的面积 $/ c m^{2}$
142
136
126
112
94
72
若等腰直角三角形的直角边长为3cm，则图中阴影部分的面积是 $c m^{2}$ ．

查看试题解析
15. 如图，在△ABC中，AB边的垂直平分线交AC边于点D．若△BCD的周长为5，BC＝2，则AC的长为．

查看试题解析
16. 在△ABC中，AB>AC，AD⊥BC于点D．以点A为圆心，以AC为半径作弧，与直线BC相交于另一点E，连接AE．若CD＝2，BC＝10，AD＝x，则△ABE的面积y与x之间的关系式为．

查看试题解析

三、解答题

17. 计算： $(x + 1) (x - 2) + (9 x^{2} + 6 x) \div 3 x$ ，其中x＝－3．

查看试题解析
18. 如图，在△ABC中，∠A＝60°，∠C＝70°，BE是△ABC的角平分线， $D E ∥ B C$ 交AB于点D，求∠1的度数．

查看试题解析
19. 现有四根长度为2cm、3cm、4cm、5cm的木棒，小明任意取一根木棒，能与长度为3cm、6cm的木棒拼成一个三角形木框的概率是多少？

查看试题解析
20. 如图，点C在线段BD上， $C E ∥ A B$ ， BC＝CE，∠ACB＝∠E．

(1)、△ABC与△DCE全等吗？说明理由；

(2)、若AB＝AC，∠B＝2∠A，求∠D的度数．

查看试题解析
21. 如图，在△ABC中，∠C＝90°．

(1)、用尺规作图法作∠CAB的平分线，交BC于点D（保留作图痕迹，不用写作法）；

(2)、在（1）的条件下，若CD＝2，点E是AB边上的一个动点，连接DE，求DE的最小值．

查看试题解析
22. 如图1，在Rt△ABC中，AC＝BC，点D在AC边上，以CD为边在AC的右侧作正方形CDEF．点P以每秒1cm的速度沿F→E→D→A→B的路径运动，连接BP、CP，△BCP的面积y（ $c m^{2}$ ）与运动时间x（秒）之间的图象关系如图2所示．

(1)、求EF的长度和a的值；

(2)、当x＝6时，连接AF，判断BP与AF的数量关系，说明理由．

查看试题解析
23. 已知 $A = {(x - 2 y)}^{2} - (x - y) (x + 2 y)$ ， $B = (2 x^{3} y - 5 x^{2} y^{2} + 2 x^{2} y + 6 x y^{3}) \div x y$ ．

(1)、化简A和B；

(2)、若变量y满足2y＋A＝B－4，求出y与x的关系式；

(3)、在（2）的条件下，求 $x (- 1 + 2 x + x y) - x (x - 1) (x + 1) - {(x - y - 2)}^{2}$ 的值．

查看试题解析
24. 直观感知和操作确认是发现几何学习的重要方式，解决下列问题．

(1)、问题情境：如图1，三个相同的三角尺拼成一个图形，直接写出图中的平行线；

(2)、问题理解：如图2，在三个相同的直角三角形拼成的一个图形中，若点M是线段BC的三等分点（其中CM>BM），点P是线段AC上的一个动点，画出BP＋PM取得最小值时点P的位置，并说明理由；

(3)、问题运用：如图3，在三个相同的直角三角形拼成的一个图形中，点M是直线BD上的一个动点，点P是线段CE上的一个动点．若AC＝a、CE＝b、AE＝c（其中a、b、c为常数），求DP＋PM的最小值．

查看试题解析

三角形的直角边/cm	1	2	3	4	5	6
阴影部分的面积 $/ c m^{2}$	142	136	126	112	94	72