广东省佛山市禅城区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 $a^{3} \cdot a^{6} = a^{9}$ C、 $a^{8} \div a^{2} = a^{4}$ D、 $3 a^{2} + 4 a^{2} = 7 a^{4}$

查看试题解析
2. 数据0.000000098用科学记数法表示为（）

A、 $9.8 \times 1 0^{8}$ B、 $9.8 \times 1 0^{7}$ C、 $9.8 \times 1 0^{- 8}$ D、 $9.8 \times 1 0^{- 7}$

查看试题解析
3. 每组数分别是三根小木棒的长度，用它们能摆成三角形的是（）

A、3cm，4cm，8cm B、8cm，7cm，15cm C、13cm，12cm，20cm D、5cm，5cm，11cm

查看试题解析
4. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，直线 $a ∥ b ， ∠ 1 = 36 °$ ，则 $∠ 2$ 等于（）

A、 $136 °$ B、 $144 °$ C、 $146 °$ D、 $152 °$

查看试题解析
6. 下列事件中是不可能事件的是（）

A、从一副扑克牌中任抽一张牌恰好是“红桃” B、在装有白球和黑球的袋中摸球，摸出了红球 C、2022年大年初一早晨艳阳高照 D、从两个班级中任选三名学生，至少有两名学生来自同一个班级

查看试题解析
7. 历史上某地曾干旱缺水，因此在全国开展了献爱心、建母亲水窖的活动，如图是某母亲水窖的横断面示意图，如果这个母亲水窖以固定的流量注水，下面能大致表示水的深度h和时间t之间的关系的图象是（）

A、 B、 C、 D、

查看试题解析
8. 如图，直线 $l ∥ m$ ，将含有45°角的三角板 $A B C$ 的直角顶点 $C$ 放在直线 $m$ 上，若 $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数为（）

A、20° B、25° C、30° D、15°

查看试题解析
9. 已知 $x + y = 3$ ， $x y = - 2$ ，则 $x^{_{2}} - x y + y^{_{2}}$ 的值是（　　）

A、11 B、15 C、3 D、7

查看试题解析
10. 甲、乙两车沿同一条路从 $A$ 地出发匀速行驶至相距 $300 k m$ 的 $B$ 地，甲出发1小时后乙再出发，如图表示甲、乙两车离开 $A$ 地的距离 $s (k m)$ 与乙出发的时间 $t (h)$ 之间的关系，下列结论错误的是（）

A、甲车的速度是 $60 k m / h$ B、乙车的速度是 $100 k m / h$ C、 $a$ 的值为60， $b$ 的值为4 D、甲车出发 $2.3 h$ 后被乙车追上

查看试题解析
11. 某小组在“用频率估计概率”的试验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的试验最有可能的是(　　)

A、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” B、掷一个质地均匀的正方体骰子，落地时面朝上的点数是6 C、一次掷两枚质地均匀的硬币，出现两枚硬币都正面朝上 D、用2，3，4三个数字随机排成一个三位数，排出的数是偶数

查看试题解析
12. 如图， $R t △ A C B$ 中， $∠ A C B = 90 °$ ， $△ A B C$ 的角平分线 $A D$ 、 $B E$ 相交于点 $P$ ，过点 $P$ 作 $P F ⊥ A D$ 交 $B C$ 的延长线于点 $F$ ，交 $A C$ 于点 $H$ ，则下列结论：① $∠ A P B = 135 °$ ；② $B F = B A$ ；③ $P H = P D$ ；④连接 $C P$ ， $C P$ 平分 $∠ A C B$ ．其中正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知3^x=5，3^y=2，则3^x+y的值是.

查看试题解析
14. 三角形的三条线交于一点，这点称为三角形的重心．

查看试题解析
15. 在直角三角形中，有一个锐角是另一个锐角的2倍，则这两个锐角分别为．

查看试题解析
16. 已知等腰三角形的两边长分别为 $4 c m$ 和 $8 c m$ ，则此三角形的周长为cm．

查看试题解析
17. 一个底面是正方形的长方体，高为6，底面正方形边长为10．如果它的高不变，底面正方形边长增加 $a$ ，那么它的体积增加．

查看试题解析
18. 如图，将一个长方形纸片 $A B C D$ ，沿着 $B E$ 折叠，使 $C$ 、 $D$ 点分别落在点 $C_{1}$ ， $D_{1}$ 处，且边 $C_{1} D_{1}$ 经过点 $A$ ，若 $∠ C_{1} B A = 50 °$ ，则 $∠ A E B =$ ．

查看试题解析

三、解答题

19. 计算：

(1)、 $| - 2 | + {(- 2)}^{2} + {(3.14 - π)}^{0} - {(\frac{1}{3})}^{- 1}$ ；

(2)、先化简，再求值： $[{(x - y)}^{2} + (x + y) (x - y)] \div 2 x$ ，其中 $x = 1$ ， $y = - 2021$ ．

查看试题解析
20. 一个不透明的箱子里装有红、黄、蓝三种颜色的小球共30个，它们除颜色外其他均相同，其中红色球有6个、黄色球有16个．

(1)、求摸出1个球是蓝色球的概率；

(2)、再往箱子中放入多少个蓝色球，可以使摸出1个蓝色球的概率为 $\frac{1}{2}$ ？

查看试题解析
21. 周末，小明坐公交车到文华公园游玩，他从家出发0.8小时后到达书城，停留一段时间后继续坐公交车到文华公园，在小明离家一段时间后，爸爸驾车沿相同的路线前往文华公园，如图是他们离家的路程 $s (k m)$ 与小明离家时间 $t (h)$ 的关系图，请根据图回答下列问题：

(1)、图中自变量是，因变量是；小明家到文华公园的路程为 $k m$ ；

(2)、小明书城停留的时间为h，小明从家出发到达文化公园的平均速度为 $k m / h$ ；

(3)、图中的 $B$ 点表示；

(4)、爸爸驾车经过多久追上小明？此时距离文华公园多远？

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、利用尺规，作 $A B$ 边的垂直平分线交 $A C$ 于点 $D$ ，交 $A B$ 于点 $E$ ；（不写作法，保留作图痕迹）

(2)、在（1）中，连接 $B D$ ，若 $∠ D B C = 27 °$ ，试求出 $∠ A$ 的度数．

查看试题解析
23. 【阅读材料】“数形结合”是一种非常重要的数学思想方法．比如：在学习“整式的乘法”时，我们通过构造几何图形，用“等积法”直观地推导出了完全平方和公式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ （如图1）．利用“数形结合”的思想方法，可以从代数角度解决图形问题，也可以用图形关系解决代数问题．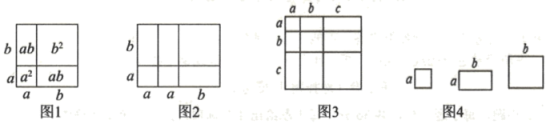

(1)、【方法应用】根据以上材料提供的方法，完成下列问题：
由图2可得等式：；由图3可得等式：；

(2)、利用图3得到的结论，解决问题：若 $a + b + c = 15$ ， $a b + a c + b c = 35$ ，则 $a^{2} + b^{2} + c^{2} =$ ；

(3)、如图4，若用其中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形， $z$ 张边长分别为 $a$ 、 $b$ 的长方形纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 长方形（无空隙、无重叠地拼接），则 $x + y + z =$ ；

(4)、如图4，若有3张边长为 $a$ 的正方形纸片，4张边长分别为 $a b$ 的长方形纸片，5张边长为 $b$ 的正方形纸片．从中取出若干张纸片，每种纸片至少取一张．把取出的这些纸片拼成一个正方形（无空隙、无重叠地拼接），则拼成的正方形的边长最长可以为．

(5)、【方法拓展】
已知正数 $a$ ， $b$ ， $c$ 和 $m$ ， $n$ ， $l$ ，满足 $a + m = b + n = c + l = k$ ．试通过构造边长为 $k$ 的正方形，利用图形面积来说明 $a l + b m + c n < k^{2}$ ．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = α$ （ $0 ° < α < 90 °$ ）， $D$ 为射线 $B C$ 上一动点（不与点 $B$ 、 $C$ 重合），在 $A D$ 的右侧作 $△ A D E$ ，使得 $A E = A D$ ， $∠ D A E = ∠ B A C$ ，连接 $C E$ ．

(1)、若 $∠ A B C = 45 °$ ，则 $∠ A D E =$ ；

(2)、当点 $D$ 在线段 $B C$ 上时，求证： $△ B A D ≌ △ C A E$ ；

(3)、若点 $D$ 运动到线段 $B C$ 上某一点时，恰好有 $A B = C D + C E$ ，问：线段 $C E$ 与线段 $A B$ 有什么位置关系并说明理由；

(4)、在点 $D$ 的运动过程中，当 $D E$ 垂直于 $△ A B C$ 的某边时，则 $∠ D E C =$ （用含 $α$ 的代数式表示）．

查看试题解析