广东省潮州市湘桥区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 下列实数是无理数的是( )A、3 B、 C、 D、02. 在下面四个图形中, 与 是对顶角的是( ).A、
 B、
B、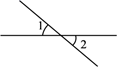 C、
C、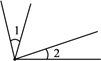 D、
D、 3. 在平面直角坐标系中,点P(-2,-1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下面调查统计中,适合采用普查方式的是( )A、华为手机的市场占有率 B、乘坐飞机的旅客是否携带了违禁物品 C、国家宝藏”专栏电视节目的收视率 D、“现代”汽车每百公里的耗油量5. 下列运算正确的是( )A、 B、 C、 D、6. 小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是( )
3. 在平面直角坐标系中,点P(-2,-1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下面调查统计中,适合采用普查方式的是( )A、华为手机的市场占有率 B、乘坐飞机的旅客是否携带了违禁物品 C、国家宝藏”专栏电视节目的收视率 D、“现代”汽车每百公里的耗油量5. 下列运算正确的是( )A、 B、 C、 D、6. 小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是( ) A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月7. 二元一次方程 有无数多个解,下列四组值中不是该方程的解的是( )A、 B、 C、 D、8. 关于 , ,2大小比较正确的是( )A、 <2< B、 < <2 C、 < <2 D、2< <9. 甲、乙、丙三种商品,若购买甲2件、乙4件、丙3件,共需220元钱,购甲3件、乙1件、丙2件共需235元钱,那么购甲、乙、丙三种商品各一件共需( )A、85元 B、89元 C、90元 D、91元10. 已知关于x,y的二元一次方程组 ,下列结论中正确的是( )
A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月7. 二元一次方程 有无数多个解,下列四组值中不是该方程的解的是( )A、 B、 C、 D、8. 关于 , ,2大小比较正确的是( )A、 <2< B、 < <2 C、 < <2 D、2< <9. 甲、乙、丙三种商品,若购买甲2件、乙4件、丙3件,共需220元钱,购甲3件、乙1件、丙2件共需235元钱,那么购甲、乙、丙三种商品各一件共需( )A、85元 B、89元 C、90元 D、91元10. 已知关于x,y的二元一次方程组 ,下列结论中正确的是( )①当这个方程组的解x,y的值互为相反数时,a=﹣1;
②当x为正数,y为非负数时,﹣ <a≤ ;
③无论a取何值,x+2y的值始终不变.
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 如果 , 那么用含y的代数式表示x,则x= .12. 如图,直线 , Rt中, , , 则 .
 13. 不等式的正整数解是 .14. 平面直角坐标系中,点在x轴上,则 .15. 一个正数的平方根是和 , 则 .16. 不等式组 有4个整数解,则m的取值范围是 .17. 如图,点 , 点 , 点 , 点 , 按照这样的规律下去,点的坐标为 .
13. 不等式的正整数解是 .14. 平面直角坐标系中,点在x轴上,则 .15. 一个正数的平方根是和 , 则 .16. 不等式组 有4个整数解,则m的取值范围是 .17. 如图,点 , 点 , 点 , 点 , 按照这样的规律下去,点的坐标为 .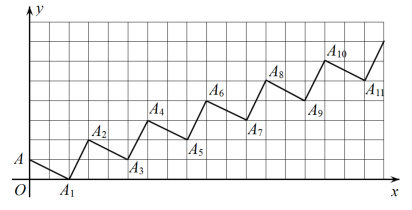
三、解答题
-
18. 计算:19. 解方程组:20. 解不等式组: ,并把解集在数轴上表示出来.
 21. △ABC在平面直角坐标系中的位置如图所示,其中 , , .
21. △ABC在平面直角坐标系中的位置如图所示,其中 , , . (1)、△ABC的面积为 . (直接写出答案)(2)、把△ABC向左平移得到了 , 已知坐标为 , 那么△ABC向左是平移了 ▲ 个单位长度得到 , 其中点的坐标为 ▲ , (直接写出答案)并请在图中画出 .22. 文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
(1)、△ABC的面积为 . (直接写出答案)(2)、把△ABC向左平移得到了 , 已知坐标为 , 那么△ABC向左是平移了 ▲ 个单位长度得到 , 其中点的坐标为 ▲ , (直接写出答案)并请在图中画出 .22. 文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:组别
年龄段
频数(人数)
第1组
5
第2组
第3组
35
第4组
20
第5组
15
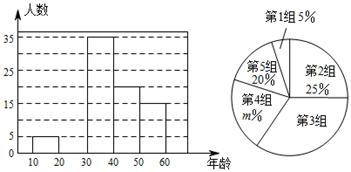 (1)、请直接写出 , , 第3组人数在扇形统计图中所对应的圆心角是度.(2)、请补全上面的频数分布直方图;(3)、假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?23. 如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.
(1)、请直接写出 , , 第3组人数在扇形统计图中所对应的圆心角是度.(2)、请补全上面的频数分布直方图;(3)、假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?23. 如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ. (1)、求证:EFBC;(2)、若FP⊥AC,∠2+∠C=90°,求证:∠1=∠B;(3)、若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.24. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备,已知3台A型设备和2台B型设备日处理能力一共为54吨;5台A型设备和1台B型设备日处理能力一共为62吨.(1)、求1台A型设备、1台B型设备日处理能力各多少吨?(2)、若购买A、B两种型号的垃圾处理设备共20台,并且它们的日处理能力不低于235吨.请你为该景区设计购买A、B两种设备的方案;(3)、已知每台A型设备价格为5万元,每台B型设备价格为7万元.厂家为了促销产品,规定货款不低于137万元时,则按9.5折优惠;问:采用(2)中设计的哪种方案,使购买费用最少,并说明理由.25. 如图,在平面直角坐标系中,点A、B的坐标分别为、 , 且实数a、b满足 .
(1)、求证:EFBC;(2)、若FP⊥AC,∠2+∠C=90°,求证:∠1=∠B;(3)、若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.24. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备,已知3台A型设备和2台B型设备日处理能力一共为54吨;5台A型设备和1台B型设备日处理能力一共为62吨.(1)、求1台A型设备、1台B型设备日处理能力各多少吨?(2)、若购买A、B两种型号的垃圾处理设备共20台,并且它们的日处理能力不低于235吨.请你为该景区设计购买A、B两种设备的方案;(3)、已知每台A型设备价格为5万元,每台B型设备价格为7万元.厂家为了促销产品,规定货款不低于137万元时,则按9.5折优惠;问:采用(2)中设计的哪种方案,使购买费用最少,并说明理由.25. 如图,在平面直角坐标系中,点A、B的坐标分别为、 , 且实数a、b满足 . (1)、求A、B两点的坐标;(2)、如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是 , 设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;(3)、如图2,在(2)的条件下,若 , 点G是第二象限中一点,并且y轴平分 . 点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究 , , 之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
(1)、求A、B两点的坐标;(2)、如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是 , 设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;(3)、如图2,在(2)的条件下,若 , 点G是第二象限中一点,并且y轴平分 . 点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究 , , 之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).