云南省昆明市县区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 在-1,-2,-3,四个数中,其中最小的数是( )A、-1 B、-2 C、-3 D、2. 下列说法中,正确的是( )A、“同位角相等”是一个真命题 B、图形的平移是指把图形沿水平方向移动 C、“凡直角都相等”是一个假命题 D、在平移的过程中,对应线段互相平行(或在同一条直线上)且相等3. 若与的和是单项式,则的算术平方根是( )A、2 B、 C、4 D、4. 下列调查方式中,选择合理的是( )A、为了了解某种灯泡的使用寿命,选择全面调查 B、调查某批次汽车的抗撞击能力,选择抽样调查 C、了解某班学生的身高情况,选择抽样调查 D、调查春节联欢晚会的收视率,选择全面调查5. 如图,小胡同学的家在点处,他在行走速度相同的情况下,想尽快地到达公路边,他选择沿线段去公路边,他这一选择用到的数学知识是( )
 A、两点之间,线段最短 B、两点之间,直线最短 C、垂线段最短 D、两点确定一条直线6. 如图, , 则图中相互平行的线段是( )
A、两点之间,线段最短 B、两点之间,直线最短 C、垂线段最短 D、两点确定一条直线6. 如图, , 则图中相互平行的线段是( ) A、// B、// C、// D、无法确定7. 如图,在长方形中, , , 点的坐标为 , 平行于轴,则点的坐标是( )
A、// B、// C、// D、无法确定7. 如图,在长方形中, , , 点的坐标为 , 平行于轴,则点的坐标是( )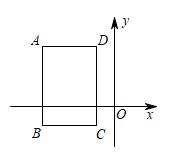 A、 B、 C、 D、8. 在平面直角坐标系中,将点向右平移3个单位长度,再向上平移2个单位长度,得到点 , 则点的坐标为( )A、 B、 C、 D、9. 一条船顺流航行,每小时行;逆流航行,每小时行 . 设轮船在静水中的速度为 , 水的流速为 . 根据题意,得到的方程组是( )A、 B、 C、 D、10. 下面解不等式的过程中,有错误的一步是( )
A、 B、 C、 D、8. 在平面直角坐标系中,将点向右平移3个单位长度,再向上平移2个单位长度,得到点 , 则点的坐标为( )A、 B、 C、 D、9. 一条船顺流航行,每小时行;逆流航行,每小时行 . 设轮船在静水中的速度为 , 水的流速为 . 根据题意,得到的方程组是( )A、 B、 C、 D、10. 下面解不等式的过程中,有错误的一步是( )①去分母,得;②去括号,得;③移项、合并同类项,得;④未知数系数化为1,得 .
A、① B、② C、③ D、④11. 一元一次不等式的解集在数轴上表示为( )A、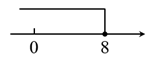 B、
B、 C、
C、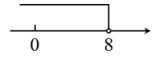 D、
D、 12. 小王在解关于 , 的二元一次方程组时,解得 , 则和分别代表的数是( )A、2,6 B、4,6 C、6,2 D、6,4
12. 小王在解关于 , 的二元一次方程组时,解得 , 则和分别代表的数是( )A、2,6 B、4,6 C、6,2 D、6,4二、填空题
-
13. 为了了解某市100000名市民对“新型冠状病毒”的了解情况,从中随机抽取了200名市民进行问卷调查,这项调查中样本容量是 .14. 如图,直线∥ , 则度.
 15. 以方程组的解为坐标的点在平面直角坐标系中的第象限.16. 已知点在轴上,则的值为 .17. 关于的不等式组有解,则的取值范围是 .18. 若规定表示一个正实数的整数部分,例如: , , 则 .
15. 以方程组的解为坐标的点在平面直角坐标系中的第象限.16. 已知点在轴上,则的值为 .17. 关于的不等式组有解,则的取值范围是 .18. 若规定表示一个正实数的整数部分,例如: , , 则 .三、解答题
-
19.(1)、计算;(2)、解不等式组 , 并将解集表示在数轴上.
 20. 如图,在平面直角坐标系中,三角形三个顶点的坐标为、、 .
20. 如图,在平面直角坐标系中,三角形三个顶点的坐标为、、 . (1)、在图中将三角形向右平移五个单位长度,再向下平移三个单位长度,得到三角形 , 请在平面直角坐标系中画出平移后的三角形;(2)、请直接写出点的坐标;(3)、求三角形的面积.21. 完成下面的证明过程,如图,BD∥GF,∠1=∠2.求证:∠DEC=∠ABC
(1)、在图中将三角形向右平移五个单位长度,再向下平移三个单位长度,得到三角形 , 请在平面直角坐标系中画出平移后的三角形;(2)、请直接写出点的坐标;(3)、求三角形的面积.21. 完成下面的证明过程,如图,BD∥GF,∠1=∠2.求证:∠DEC=∠ABC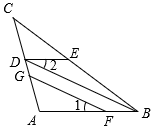
证明:∵BD∥GF( )
∴∠1= ▲ (两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠2= ▲ ( )
∴DE∥AB( )
∴∠DEC=∠ABC( )
22. 某校想要了解全校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取了本校部分学生进行调查,以了解学生喜欢收看哪个电视节目,并将调查结果绘制成了两幅不完整的统计图,其中,“新闻”类节目的喜爱比例为10%.请结合绘制图中的信息,解答下列问题: (1)、本次共抽查了名学生,扇形统计图中“动画”类节目的喜爱比例为;(2)、请将条形统计图补充完整;(3)、该校共有2000名学生,根据调查数据估计该校有多少名学生喜欢收看“动画”电视节目.
(1)、本次共抽查了名学生,扇形统计图中“动画”类节目的喜爱比例为;(2)、请将条形统计图补充完整;(3)、该校共有2000名学生,根据调查数据估计该校有多少名学生喜欢收看“动画”电视节目.