云南省昆明市盘龙区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 要调查下列问题,适合采用全面调查(普查)的是( )A、中央电视台《开学第一课》的收视率 B、昆明市居民6月份人均网上购物的次数 C、神舟十三号载人飞船的零部件质量 D、某品牌新能源汽车的最大续航里程2. 下列计算正确的是( )A、 B、 C、 D、3. 已知 , 下列不等式成立的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 不等式组 的解集在数轴上用阴影表示正确的是( )A、
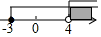 B、
B、 C、
C、 D、
D、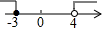 6. 如图,△ABC中,∠ABC=90°沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( )
6. 如图,△ABC中,∠ABC=90°沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( ) A、EC=CF B、∠DEF=90° C、AC=DF D、ACDF7. 若关于、的方程组的解满足 , 则的值是( )A、4 B、 C、2 D、18. 如图,添加下列条件可使直线的是( )
A、EC=CF B、∠DEF=90° C、AC=DF D、ACDF7. 若关于、的方程组的解满足 , 则的值是( )A、4 B、 C、2 D、18. 如图,添加下列条件可使直线的是( ) A、 B、 C、 D、9. 某中学就周一早上学生到校的方式问题,对八年级的所有学生进行了一次调查,并将调查结果制作成了如下表格,则步行到校的学生频率是( )
A、 B、 C、 D、9. 某中学就周一早上学生到校的方式问题,对八年级的所有学生进行了一次调查,并将调查结果制作成了如下表格,则步行到校的学生频率是( )八年级学生人数
步行人数
骑车人数
乘公交车人数
其他方式人数
300
75
12
135
78
A、0.1 B、0.25 C、0.3 D、0.4510. 如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线 上,斜边AB平分 ,交直线GH于点E,则 的大小为( ) A、 B、 C、 D、11. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、12. 已知关于的不等式组的整数解共有5个,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、11. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、12. 已知关于的不等式组的整数解共有5个,则的取值范围是( )A、 B、 C、 D、二、填空题
-
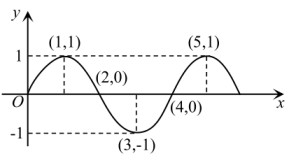
13. 在实数 , 0, , 中,最小的数是 .14. 在平面直角坐标系中,点在轴上,点在轴上,且横坐标为 , 则点的坐标为 .15. 将一张面值为50元的人民币,兑换成10元或20元的零钱,有种兑换方案.16. 下列三个命题:①两个角的和等于平角时,这两个角互为邻补角;②两直线平行,内错角相等;③同旁内角互补,它们是真命题的是 . (填序号)17. 为配合“禁烟”行动.某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对—题记10分.答错(或不答)一题记 一5分.小明参加本次竞赛得分要超过100分.他至少要答对道题.18. 如图,动点在平面直角坐标系中,沿曲线的方向从左往右运动,第1秒从原点运动到点(1,1),第2运动到点(2,0),第3秒运动到点(3,-1),第4秒运动到点(4,0)按这样的规律,第2022秒运动到点的坐标是 .
三、解答题
-
19.(1)、计算:;(2)、解方程组:;(3)、解不等式组 , 并写出它的最小整数解.20. 第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,将于2022年2月4日开幕,共设7个大项,15个分项,109个小项.学校从七年级同学中随机抽取若干名,组织了奥运知识竞答活动,将他们的成绩进行整理,得到如下不完整的频数分布表、频数分布直方图与扇形统计图.(满分为100分,将抽取的成绩分成A,B,C,D四组,每组含最大值不含最小值)
分组
频数
A:60~70
4
B:70~80
12
C:80~90
16
D:90~100
△
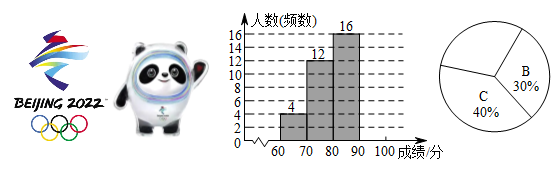 (1)、本次知识竞答共抽取七年级同学名,D组成绩在扇形统计图中对应的圆心角为°;(2)、请将频数分布直方图与扇形统计图补充完整;(3)、学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.21. 如图,在平面直角坐标系中,点A、B、C的坐标分别为 , , . 将先向左平移4个单位,再向下平移2个单位得到 .
(1)、本次知识竞答共抽取七年级同学名,D组成绩在扇形统计图中对应的圆心角为°;(2)、请将频数分布直方图与扇形统计图补充完整;(3)、学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.21. 如图,在平面直角坐标系中,点A、B、C的坐标分别为 , , . 将先向左平移4个单位,再向下平移2个单位得到 .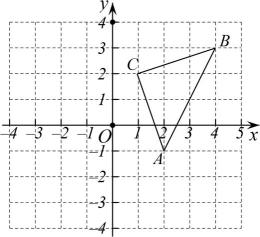 (1)、请在图中画出;(2)、写出平移后的三个顶点的坐标:( , )( , )( , )(3)、求的面积.22. 如图,在中,点在边上, , 分别交、于点、 , 平分 , 交于点 , .
(1)、请在图中画出;(2)、写出平移后的三个顶点的坐标:( , )( , )( , )(3)、求的面积.22. 如图,在中,点在边上, , 分别交、于点、 , 平分 , 交于点 , .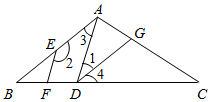 (1)、求证:;(2)、若 , 求的度数.23. 为加快复工复产,某企业需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输600箱:5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车运输一次所需费用为5000元,每辆小货车运输一次所需费用为3000元,若大货车的数量不少于6辆,总费用小于54000元.请列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?24. 在平面直角坐标系中,已知点 , , , 且满足 , 线段交轴于点 , 点是轴正半轴上的一点.
(1)、求证:;(2)、若 , 求的度数.23. 为加快复工复产,某企业需运输一批物资,据调查得知,2辆大货车与3辆小货车一次可以运输600箱:5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车运输一次所需费用为5000元,每辆小货车运输一次所需费用为3000元,若大货车的数量不少于6辆,总费用小于54000元.请列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?24. 在平面直角坐标系中,已知点 , , , 且满足 , 线段交轴于点 , 点是轴正半轴上的一点.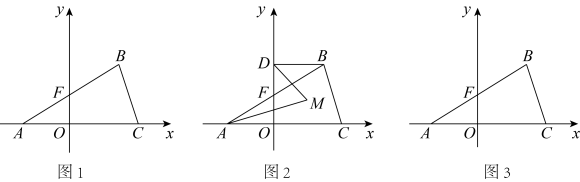 (1)、如图1,求出点、的坐标;(2)、如图2,若 , , 且、分别平分、 , 求的度数;(用含的代数式表示);(3)、如图3,坐标轴上是否存在一点 , 使得的面积是的面积的一半?若存在,求出点坐标;若不存在,请说明理由.
(1)、如图1,求出点、的坐标;(2)、如图2,若 , , 且、分别平分、 , 求的度数;(用含的代数式表示);(3)、如图3,坐标轴上是否存在一点 , 使得的面积是的面积的一半?若存在,求出点坐标;若不存在,请说明理由.