山东省济南市钢城区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是二元一次方程的是（）

A、 $x y = 1$ B、 $x^{2} + y^{2} = 1$ C、 $2^{x + y} = 1$ D、 $x + y = 0$

查看试题解析
2. 下列事件是随机事件事件的是（）

A、瓜熟蒂落 B、水中捞月 C、守株待兔 D、缘木求鱼

查看试题解析
3. 若 $x > y$ ，下列各式不一定成立的是（）

A、 $x^{2} > y^{2}$ B、 $- x < - y$ C、 $2 x > 2 y$ D、 $x - 2 > y - 2$

查看试题解析
4. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x、y的方程 $x - a y = 3$ 的一个解，则a的值是（）

A、3 B、-3 C、-1 D、1

查看试题解析
5. 如图，有一块含有30°角的直角三角板的两个顶点放在直尺的对边上，如果 $∠ 2 = 43 °$ ，那么 $∠ 1$ 的度数是（）

A、18° B、17° C、16° D、15°

查看试题解析
6. 如图，有5张形状、大小、材质均相同的卡片，正面分别印着北京2022年冬奥会的越野滑雪、速度滑冰、花样滑冰、高山滑雪、单板滑雪大跳台的体育图标，背面完全相同．现将这5张卡片洗匀并正面向下放在桌上，从中随机抽取一张，抽出的卡片正面恰好是“滑冰”项目的图案的可能性是（）．

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 如图，在△ $A B C$ 与 $△ D F E$ 中， $A C = D E$ ， $∠ A C B = ∠ D E F$ ，添加下列条件后，仍不能得到 $△ A B C ≌ △ D F E$ 的是（）

A、 $∠ B = ∠ F$ B、 $B E = C F$ C、 $∠ A = ∠ D$ D、 $A B = D F$

查看试题解析
8. 如图，直线y＝kx＋b（k≠0）经过点（－1，3），则不等式kx＋b≥3解集为（）

A、x≤－1 B、x≥－1 C、x≤3 D、x≥3

查看试题解析
9. 已知，如图， $A B ∥ C D$ ， $∠ A = 95 °$ ， $∠ C = 65 °$ ， $∠ 1 ： ∠ 2 = 3 ： 4$ ，则 $∠ B$ 的度数为（）

A、56° B、45° C、36° D、24°

查看试题解析
10. 如图，在 $△ A B C$ 中，P为边 $A B$ 上的一点，分别以P、C为圆心，以大于 $P C$ 一半为半径画弧，两弧交点连线交 $A C$ 于E，已知 $A C = 6$ ， $A P = 3$ ，则 $△ A P E$ 的周长是（）

A、6 B、7 C、9 D、12

查看试题解析
11. 若 $| 2 x + y + 8 | + (x - 2 y)^{2} = 0$ ，则 $3 x - y$ 的值是（）

A、-6 B、-8 C、-10 D、-12

查看试题解析
12. 定义：对于实数a，符号 $[a]$ 表示不大于a的最大整数．例如： $[5.7] = 5$ ， $[5] = 5$ ， $[- π] = - 4$ ．如果 $[\frac{x}{2}] = - 3$ （）

A、 $- 6 ⩽ x < - 4$ B、 $- 8 ⩽ x < - 6$ C、 $- 6 < x ⩽ - 4$ D、 $- 8 < x ⩽ - 6$

查看试题解析

二、填空题

13. 一个不透明的口袋中放着若干个黑球和红球，这两种球除了颜色以外没有任何其它区别，袋中的球已经搅匀，从口袋中随机取出一个球，取出黑球的概率是 $\frac{1}{4}$ ，如果袋中共有20个小球，那么袋中的黑球的个数为．

查看试题解析
14. 三角形的任意两边之和大于第三边是命题．（填写真或假）

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C$ 的平分线交 $A C$ 于点D，过点D作 $D E ∥ B C$ 交 $A B$ 于点E．若 $∠ A = 70 °$ ， $∠ C = 50 °$ ，求 $∠ B D E =$ ．

查看试题解析
16. 《九章算术》是中国古代第一部数学专著，也是世界上最早的印刷本数学书它的出现标志着中国古代数学体系的形成．《九章算术》早在隋唐时期即已传入朝鲜、日本并被译成日、俄、德、法等多种文字版本，书中有如下问题：今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？设有x人，该物品价值y元，可得出关于x，y的二元一次方程组为．

查看试题解析
17. 等腰三角形一腰上的高与另一腰的夹角为38°，则该等腰三角形的底角的度数为

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点D，点E、F分别在 $A D$ 、 $A C$ 上，则 $C E + E F$ 的最小值为．

查看试题解析

三、解答题

19. 解方程组： ${\begin{array}{l} \end{array} \begin{matrix} x + 2 y = 1 \\ 3 x - 2 y = 11 \end{matrix}$ .

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 (x + 2) > x \\ 1 - 2 x \geq \frac{x + 7}{2} \end{array}$ ，并求出它的整数解．

查看试题解析
21. 如图， $∠ B A C = 90 °$ ， $A D$ 是 $∠ B A C$ 内部一条射线，若 $A B = A C$ ， $B E ⊥ A D$ 于点E， $C F ⊥ A D$ 于点F．求证： $△ A B E ≌ △ C A F$ ．

查看试题解析
22. 一个小球在如图所示的方格地板上自由地滚动，并随机停留在某块地板上，每块地板大小、质地完全相同．

(1)、该小球停留在黑色区域的概率是多少？

(2)、甲，乙两人比赛，小球落到白色区域甲赢，落在黑色区域乙赢，你认为这个游戏公平吗？

查看试题解析
23. 如图，已知 $∠ 1 = ∠ B D C$ ， $∠ 2 + ∠ 3 = 180 °$ ．

(1)、求证： $A D ∥ C E$ ；

(2)、若 $D A$ 平分 $∠ B D C$ ， $C E ⊥ A E$ 于E， $∠ 1 = 52 °$ ，求 $∠ F A B$ 的度数．

查看试题解析
24. 某生态体验园推出了甲、乙两种消费卡，设入园次数为x时所需费用为y元，选择这两种卡消费时，y与x的函数关系如图所示，解答下列问题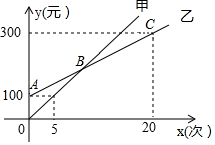

(1)、分别求出选择这两种卡消费时，y关于x的函数表达式；

(2)、请根据入园次数确定选择哪种卡消费比较合算．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点E是 $A B$ 边的中点，点F，G分别在 $A C$ ， $B C$ 上，且 $E F ⊥ E G$ ．

(1)、求证： $A F = C G$ ；

(2)、若 $A C = 2$ ，求四边形 $C F E G$ 的面积．

查看试题解析
26. 冰墩墩和雪容融分别是2022年北京冬奥会和冬残奥会的吉祥物，王老师准备从某电商平台购进这两种吉祥物奖励给学生．已知购买3个冰墩墩和2个雪容融需要380元，购买1个冰墩墩和2个雪容融需要220元．

(1)、冰墩墩和雪容融的单价分别是多少元？

(2)、王老师计划共购买100个吉祥物，其中雪容融的数量不超过冰墩墩数量的2倍，通过计算，你知道王老师最少需要准备多少钱吗？

查看试题解析
27.

(1)、已知：如图，△ABC为等边三角形，点D为BC边上的一动点（点D不与B、C重合），以AD为边作等边△ADE，连接CE．

求证：① $B D = C E$ ；

② $∠ D C E = 120 °$ ；

(2)、如图，在△ABC中， $∠ B A C = 90 °$ ， $A C = A B$ ，点D为BC上的一动点（点D不与B、C重合），以AD为边作等腰Rt△ADE， $∠ D A E = 90 °$ （顶点A、D、E按逆时针方向排列），连接CE，类比题（1）请你猜想：
①∠DCE的度数；

②线段BD、CD、DE之间的关系，并说明理由；

(3)、如图，在（2）的条件下，若D点在BC的延长线上运动，以AD为边作等腰Rt△ADE， $∠ D A E = 90 °$ （顶点A、D、E按逆时针方向排列），连接CE；
①则题（2）的结论还成立吗？请直接写出，不需论证；

②连结BE，若 $B E = 10$ ， $B C = 6$ ，直接写出AE的长．

查看试题解析