辽宁省沈阳市于洪区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、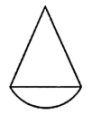 C、
C、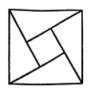 D、
D、 2. 中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下某种疟原虫平均长度为米,将数据用科学记数法可表示为( )A、 B、 C、 D、3. 如图,下列条件不能判定AB∥CD的是( )
2. 中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下某种疟原虫平均长度为米,将数据用科学记数法可表示为( )A、 B、 C、 D、3. 如图,下列条件不能判定AB∥CD的是( ) A、∠1=∠3 B、∠1=∠2 C、∠2=∠3 D、∠2+∠4=180°4. 下列计算正确的是( )A、 B、 C、 D、5. 下列事件为必然事件的是( )A、翻开数学书,恰好翻到第16页 B、两条线段可以组成一个三角形 C、400人中有两人的生日在同一天 D、掷一枚质地均匀的骰子,朝上一面的点数是76. 若购买水性笔10支,花费20元,用y(元)表示购买水性笔的花费,x(支)表示水性笔的支数,那么y与x之间的关系式是( )A、 B、 C、 D、7. 某射击运动员在同一条件下的射击,结果如下表:
A、∠1=∠3 B、∠1=∠2 C、∠2=∠3 D、∠2+∠4=180°4. 下列计算正确的是( )A、 B、 C、 D、5. 下列事件为必然事件的是( )A、翻开数学书,恰好翻到第16页 B、两条线段可以组成一个三角形 C、400人中有两人的生日在同一天 D、掷一枚质地均匀的骰子,朝上一面的点数是76. 若购买水性笔10支,花费20元,用y(元)表示购买水性笔的花费,x(支)表示水性笔的支数,那么y与x之间的关系式是( )A、 B、 C、 D、7. 某射击运动员在同一条件下的射击,结果如下表:射击总次数n
10
20
50
100
200
500
1000
击中靶心的次数m
9
16
41
88
168
429
861
击中靶心的频率
0.90
0.8
0.82
0.88
0.84
0.858
0.861
根据频率的稳定性,估计这名运动员射击一次时击中靶心的概率约是( )
A、0.90 B、0.82 C、0.84 D、0.8618. 将变形正确的是( )A、 B、 C、 D、9. 声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:气温(℃)
0
5
10
15
20
音速()
331
334
337
340
343
下列结论错误的是( )
A、在变化中,气温是自变量,音速是因变量 B、音速随气温的增大而增大 C、当气温为5℃时,音速为 D、当气温为30℃时,音速为10. 长为 , 宽为()的长方形,若将长增加 , 宽减少 , 则它的面积会( )A、变小 B、变大 C、不变 D、无法确定二、填空题
-
11. 计算: =.12. 已知∠α与∠β互余,且∠α=40°,则∠β的度数为 .13. 如下图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是 , 理由是 .
 14. 某商场假日期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重新转动).若某顾客转动一次转盘,则其中奖的概率为 .
14. 某商场假日期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重新转动).若某顾客转动一次转盘,则其中奖的概率为 . 15. 如图,将一张长方形纸条折叠,若 , 则的度数为°.
15. 如图,将一张长方形纸条折叠,若 , 则的度数为°. 16. 在中,是边上的高,是边上的高, , 所在直线交于点F,若 , , , 则的面积为 .
16. 在中,是边上的高,是边上的高, , 所在直线交于点F,若 , , , 则的面积为 .三、解答题
-
17. 计算:(1)、;(2)、(3)、先化简,再求值: , 其中 , .18. 在3×3的正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形称为格点三角形,图中是一个格点三角形,请在下列网格中各画一个与成轴对称的格点 , 并画出其对称轴l
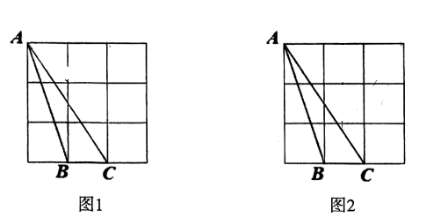 19. 已知,如图, .
19. 已知,如图, . (1)、用尺规作的一条角平分线(保留作图痕迹,不写作法,写出结论);(2)、若 , , 则°20. 补全下面推理过程:
(1)、用尺规作的一条角平分线(保留作图痕迹,不写作法,写出结论);(2)、若 , , 则°20. 补全下面推理过程:如图,AB∥CD,点E为两平行线间的一点,且 . 若 , 求的度数.
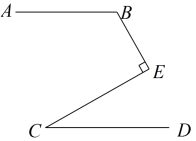
解:如下图,过点E作射线EF∥CD.

∴ ▲ =( ).
∵ ,
∴ ▲ °(垂直的定义)
∴ ▲ °
∵EF∥CD,AB∥CD
∴AB∥EF( )
∴ ▲ °( )
∴ ▲ °
21. 甲袋中有红球8个、白球5个和黑球12个;乙袋中有红球18个、白球9个和黑球23个.(每个球除颜色外都相同)(1)、若从中任意摸出一个球是红球,选哪袋成功的机会大?请说明理由;(2)、“从乙袋中取出10个红球后,乙袋中的红球个数和甲袋中红球个数一样多,所以此时若从中任意摸出一个球是红球,选甲、乙两袋成功的机会相同”.你认为这种说法正确吗?为什么?22. 如图,AC∥BD,连接 , 交于点O,若O为中点. (1)、求证:;(2)、连接 , 若 , , 若的长是偶数,则长为 .23. 数学兴趣小组的李舒和林涵两位同学将连续的正整数1,2,3,…排成如图所示的数表,从中框出某些数,做了如下探索:
(1)、求证:;(2)、连接 , 若 , , 若的长是偶数,则长为 .23. 数学兴趣小组的李舒和林涵两位同学将连续的正整数1,2,3,…排成如图所示的数表,从中框出某些数,做了如下探索: (1)、李舒在数表中框出“十”字形,并将相对的两数相乘,再左右积与上下积作差,请你帮忙完成研究过程.
(1)、李舒在数表中框出“十”字形,并将相对的两数相乘,再左右积与上下积作差,请你帮忙完成研究过程.①计算: ▲ , ▲ , 不难发现,结果都是 ▲ ;
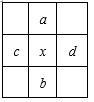
②验证:下图是从上图中取出的一部分,`在选中的五个数中,若设中心数为x,则a,b,c,d所对应的数分别 ▲ , ▲ , ▲ , ▲ (用含x的代数式表示),请你利用整式的运算,对①中的发现进行推理验证;
 (2)、林涵在数表中框出“T”字形,并将顶端左右两数相乘,再与底端数平方作差,即下图中 , 若计算的结果是-541,求林涵框出“T”字形的五个数中的最小数字.
(2)、林涵在数表中框出“T”字形,并将顶端左右两数相乘,再与底端数平方作差,即下图中 , 若计算的结果是-541,求林涵框出“T”字形的五个数中的最小数字.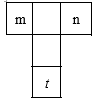 24. 如图1,在中,于点D, , , 动点E从点B出发,沿射线以的速度匀速运动,到达点D时停留1s后以原速度继续运动.如图2为的面积S()随时间t(s)的变化图像.
24. 如图1,在中,于点D, , , 动点E从点B出发,沿射线以的速度匀速运动,到达点D时停留1s后以原速度继续运动.如图2为的面积S()随时间t(s)的变化图像.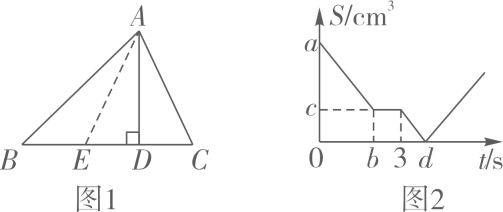 (1)、填写图2中数据:a= , b= , c= , d=;(2)、当s时,为的中线;(3)、当s时,;(4)、当动点E从点B出发时,动点F同时从点C沿边以的速度向终点B运动,当点F到达终点B后,点E也随之停止运动.当s时, .25. 已知,射线和射线相交于点B,(),且 . 点D是射线上的动点(点D不与点C和点B重合),作射线 , 并在射线上取一点E,使 , 连接 , .(1)、如下图,当点D在线段上,与的数量关系为;
(1)、填写图2中数据:a= , b= , c= , d=;(2)、当s时,为的中线;(3)、当s时,;(4)、当动点E从点B出发时,动点F同时从点C沿边以的速度向终点B运动,当点F到达终点B后,点E也随之停止运动.当s时, .25. 已知,射线和射线相交于点B,(),且 . 点D是射线上的动点(点D不与点C和点B重合),作射线 , 并在射线上取一点E,使 , 连接 , .(1)、如下图,当点D在线段上,与的数量关系为; (2)、如下图,当点D在线段上,时,在射线上取一点F,使 , 连接 , 请判断与的数量关系和位置关系,并证明你的结论;
(2)、如下图,当点D在线段上,时,在射线上取一点F,使 , 连接 , 请判断与的数量关系和位置关系,并证明你的结论;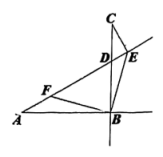 (3)、如下图,当时,探究后直接写出的度数.
(3)、如下图,当时,探究后直接写出的度数.